Несмотря на отсталость такой «первобытной» математики, цивилизованным людям тоже приходится иметь дело с эквивалентом «аибааги». В какой-то степени туземное «много» сродни нашей бесконечности. Как вы думаете, сильно ли отличаются две величины: ∞ и ∞+1? C точки зрения обычного человека, первая величина на единицу меньше второй. Но для математиков эти две величины одинаковы. Представьте себе, рассуждают они, гостиницу с бесконечным количеством номеров, где в каждом номере живёт постоялец (для такого отеля придумали даже термин «Гранд-отель Гильберта»). Как найти место для ещё одного гостя? Очень просто, нужно поселить его в первый номер, а проживающего там клиента попросить переехать во второй номер, второго — в третий и так далее. В гостинице новых номеров не прибавилось, но место для приезжего нашлось, а значит, ∞ = ∞+1.
Всё же не все бесконечные множества оказались одинаковыми, и для их измерения ввели понятие мощности. Скажем, минимально возможным из всех бесконечных множеств, «счётным», принято считать мощность множества натуральных чисел (положительных и целых). А вот множество действительных чисел (рациональных, которые можно выразить в виде правильной дроби, и иррациональных, которые в таком виде не выражаются), хотя и бесконечное, но уже больше «счётного», и его мощность обозначают как «континуум». Таким способом математики измеряют бесконечные множества почти полтора века, хотя точность подобной методики напоминает в некоторой мере математику туземцев пираха.
На практике люди бесконечностью считают то, что трудно поддаётся счёту, — помните, у Ломоносова: «Открылась бездна звезд полна, звездам числа нет, бездне — дна». Астрономы давно подсчитали число видимых невооружённым глазом звёзд и даже занесли их в справочники, но для обывателя звёзд на небе по-прежнему «аибааги» — много. Если же вдруг в небе появится новая звезда, их число увеличится на одну. Но всё равно их останется «аибааги».
Доктор физико-математических наук Ярослав Сергеев, профессор Нижегородского государственного университета им. Н. И. Лобачевского, предложил ввести для измерения бесконечных множеств другую меру. Он обозначил количество всех натуральных чисел 1, 2, 3 и т.д. специальным термином — «гросс-единицей» (от английского gross one — крупная единица) и ввёл для него специальный символ —  . Отличается «гросс-единица» от такой меры, как мощность, тем, что позволяет точнее различать бесконечные множества. Мощность множества натуральных чисел (1, 2, 3 и т.д.) и натуральных чисел больше единицы (2, 3, 4 и т.д.) одинаковая — счётная. А с позиций «гросс-единицы» второе множество измеряется величиной
. Отличается «гросс-единица» от такой меры, как мощность, тем, что позволяет точнее различать бесконечные множества. Мощность множества натуральных чисел (1, 2, 3 и т.д.) и натуральных чисел больше единицы (2, 3, 4 и т.д.) одинаковая — счётная. А с позиций «гросс-единицы» второе множество измеряется величиной  – 1. И оно содержит на единицу меньше элементов, чем первое.
– 1. И оно содержит на единицу меньше элементов, чем первое.
С «гросс-единицей» можно выполнять все арифметические действия: складывать, вычитать, умножать и делить на целые числа, для неё действуют привычные арифметические правила:
 +a=a+
+a=a+ ;
;
 +
+ =2×
=2× ;
;
0 × =
= ×
× =
= ;
;
 –
– =0;
=0;
 :
: =1;
=1;
 0=1;
0=1;
1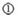 =1.
=1.
Для нового числа действует правило: часть всегда меньше целого:  <
< +1.
+1.
Удивительно, но при подобном подходе к измерению бесконечных величин не удаётся найти противоречий. По крайней мере, вот уже несколько лет новое число благополучно сосуществует с традиционной бесконечностью ∞. Более того, с помощью «гросс-единицы» можно измерять и другие, прежде бесконечные величины. Например, количество чётных чисел будем обозначать как  /2. Тогда количество всех нечётных чисел составит
/2. Тогда количество всех нечётных чисел составит  –
– /2=
/2= /2.
/2.
Впрочем, с чего это мы решили, что количество чётных и нечётных чисел одинаково? Если хотите, можете считать, что чётных чисел на одно больше. Тогда, обозначив X количество нечётных чисел, получаем, что X+1 — количество чётных чисел, а их общее количество как раз «гросс-единица»:
X+(X+1)= .
.
Решая это несложное уравнение привычными методами, получаем, что ( –1):2 — количество нечётных чисел, а (
–1):2 — количество нечётных чисел, а ( +1):2 — чётных.
+1):2 — чётных.
И опять не удаётся найти (по крайней мере, вот уже несколько лет) никакого противоречия при подобном подходе. Если и впредь не удастся доказать, что количество чётных чисел совпадает с количеством нечётных чисел, придётся подобное утверждение принимать как аксиому.
«Гросс-единица» позволяет навести порядок в бесконечных величинах, для измерения которых прежде использовали понятие «мощности множества». Скорее всего, бюджет государства, способного выстроить «Гранд-отель Гильберта», тоже бесконечен. Как удобно было бы управляться с ним, даже если бы он был минимально возможным — «счётным» бюджетом. Выделяй 90% средств на социальные нужды, всё равно на другие бюджетные статьи останется «счётное» количество денег. С помощью «гросс-единицы» можно вести «бухгалтерский учёт» даже при бесконечном бюджете, размер которого иному туземцу покажется «аибааги».
Пользоваться «гросс-единицей» уже научили компьютер: создана первая программа-калькулятор, которая выполняет арифметические действия как с конечными числами, так и с «гросс-единицей». Использование открывает возможности оперировать на компьютере не только с бесконечно большими, но и с бесконечно малыми величинами.
Работа с «гросс-единицей» не сильно отличается от обычных алгебраических преобразований. Например, легко упростить выражение:
( –1)×(
–1)×( +1)=
+1)= 2–1.
2–1.
По смыслу это значит примерно следующее: «гросс-единица» сопоставима с количеством натуральных чисел, а  2–1 — это почти «гросс-единица» в квадрате. Ну если быть совсем точным, то на единицу поменьше. Это значительно больше, чем просто
2–1 — это почти «гросс-единица» в квадрате. Ну если быть совсем точным, то на единицу поменьше. Это значительно больше, чем просто  .
.
Точно так же можно измерять и малые величины, например 1/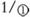 .
.
Подобный подход позволяет упростить расчёты в теории пределов. Легко посчитать, к чему стремится выражение :
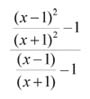
при x, стремящемся к ∞. Достаточно вместо x подставить «гросс-единицу» и выполнить с ней обычные алгебраические преобразования:
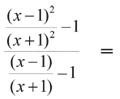
=1+( –1)/(
–1)/( +1) =2–2/(
+1) =2–2/( +1).
+1).
Сразу видно, что результат незначительно отличается от 2.
Любопытные результаты можно получить, если предложить компьютеру использовать в вычислениях «гросс-единицу». Например, выяснить, чему равно
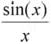
при x, близких к 0. Вычисляя значения sin(1/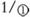 ), компьютер воспользуется формулой Тейлора:
), компьютер воспользуется формулой Тейлора:
sin(1/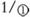 )=1/
)=1/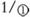 –1/(6
–1/(6 3)+…, а значит,
3)+…, а значит,
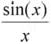 = (1/
= (1/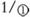 –1/(6
–1/(6 3)+…):(1/
3)+…):(1/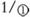 )= 1–1/(6
)= 1–1/(6 4)+…
4)+…
Для человека результат незначительно отличается от 1, а компьютер, который научили пользоваться «гросс-единицей», сможет выделить существенную часть и бесконечно малый «остаток».
Пока трудно сказать, насколько широко будет использоваться «гросс-единица». Можно только утверждать, что новое понятие позволяет по-другому взглянуть на бесконечность, а заодно и научить компьютер обращаться с ней.




