Полезная геометрия

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Вешаем зеркало

Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А₁В₁ — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.

Завариваем чай

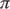
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d²).

Выдерживаем прямые углы

Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.

Строим прямой угол на земле

Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.

Проверяем перпендикулярность стен

Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.

Отмеряем нужный объём

Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.

Укрепляем калитку

Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

Выбираем табурет

Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.

Исправляем ошибку кроя

Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.

Находим середину

Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).