Пять лет назад я опубликовал две связанные статьи в журнале «Наука и жизнь»: «Правило транзитивности против нетранзитивности выбора» (№ 3, 2017) и «Нетранзитивность превосходства: продолжение темы» (№ 7, 2017). В них шла речь о нетранзитивных отношениях превосходства, метафорически называемых отношениями «камень, ножницы, бумага»: в одноимённой игре камень побеждает ножницы, те — бумагу, а бумага побеждает камень. В математике давно известны, активно изучаются и популяризуются нетранзитивные игральные кубики с такими числами на гранях, что кубик А чаще выигрывает у кубика В (показывает большее число на верхней грани), чем проигрывает ему; кубик В чаще выигрывает у С, а С чаще выигрывает у A*.
Вопрос — а можно ли изобрести механизмы, механические игрушки, взаимодействующие по принципу «камень, ножницы, бумага»? Эта тема была затронута в моих статьях в «Науке и жизни», здесь же я напишу о возможных ответах подробнее.
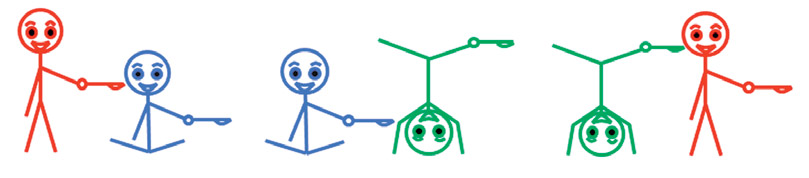
Нетранзитивные «мартышки». Посмотрев на рисунок, можно убедиться, эти три мартышки кормят друг друга нетранзитивным образом (красная — синюю, синяя — зелёную, а та — красную).
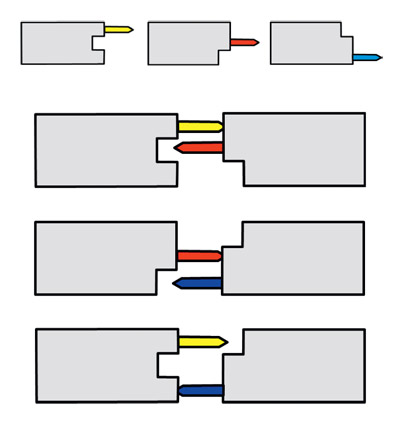
Нетранзитивные «помечальщики». Мартышки при кормлении могут ненароком закапать друг друга едой из ложки. Сделаем эту функцию основной. Из деталей «LEGO DUPLO®» с просверленными отверстиями и вставленными в них фломастерами можно соорудить такие три конструкции, что первая конструкция будет помечать своим фломастером вторую, оставаясь непомеченной ею, вторая — помечать третью, а третья — первую.

Нетранзитивные гребёнки. Кончик фломастера напоминает клин. Разовьём идею применения клиньев. Можно ли использовать клин как наклонную плоскость для таких нетранзитивных механизмов, при взаимодействии которых один поднимает другой? Возможный вариант показан на рисунке.
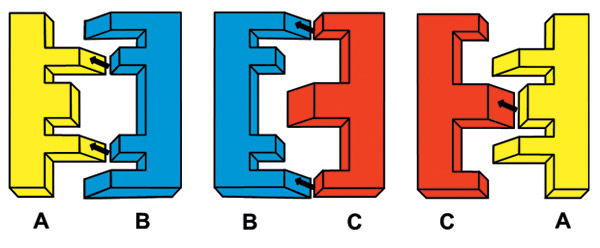

При фронтальном «наезде» гребёнка А своим профилем зубьев поднимает гребёнку В (она «сильнее»), В поднимает С, С поднимает А.
Нетранзитивные конструкции с рычагами. Перейдём к другому типу простых механизмов — рычагам. На рисунке показаны конструкции с креплением на валу длинных и коротких рычагов на разных уровнях. При равном усилии соревнующихся участников, приложенном к валам, конструкция А «пересиливает» В, В «пересиливает» С, С «пересиливает» А. Почему так происходит, читатель может подумать сам.
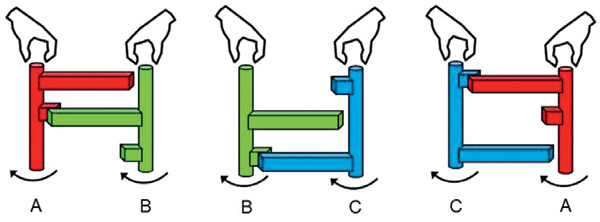
Можно устроить соревнование с использованием этих конструкций (назовём их двойными рычагами). Один участник выбирает какой-то понравившийся ему двойной рычаг. Второй участник, разбирающийся в механике, пусть и физически более слабый (например, в силу возраста), всегда может выбрать другой рычаг, который победит (пересилит) первый.
Нетранзитивные шестерни. Шестерни — ближайшие родственники рычагов в отношении способа передачи усилия. На рисунке показаны конструкции с бóльшими и меньшими шестернями, закреплёнными на валах на разных уровнях (так же, как в двойных рычагах). При попарных соединениях конструкция А вращается быстрее В в паре А-В, В вращается быстрее С в паре В-С, С вращается быстрее А в паре А-С. Если соединить все три конструкции вместе, вращаться они не смогут — их заклинит.
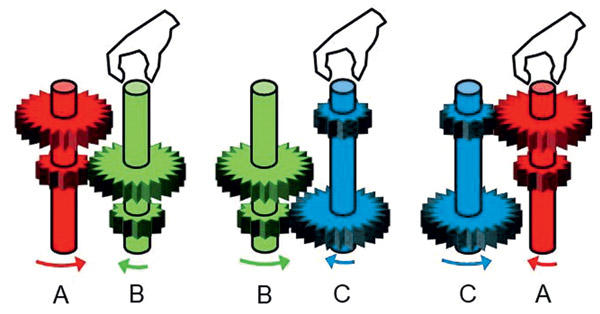
Действующую модель можно собрать из деталей детского конструктора «Gigo Junior Engineer 7333P Magic Gears» (с доработкой, поскольку оригинальные шестерни вращались на валах свободно — я закрепил их небольшими шурупами, а валы, наоборот, в плате не вращались — входили с усилием, и пришлось немного рассверлить отверстия).

Нетранзитивные шестерни с храповыми колёсами. Оскар ван Девентер, голландский изобретатель механических головоломок, сославшись на меня и взяв эту схему шестерён как базовую, придумал продвинутую версию — нетранзитивные шестерни с храповыми колёсами («Non-transitive gears»). Какую бы рукоятку ни начал вращать играющий, одна из оставшихся рукояток будет вращаться в 2 раза быстрее выбранной, а другая — в 2 раза медленнее. И заклиниваний там нет (из-за того, что шестерни соединены не напрямую, а через храповые колёса).

Поэкспериментировав с этой головоломкой, я обнаружил, что она может использоваться для игры втроём! Если два первых участника игры выберут каждый по элементу (рукоятке или шестерне), третий участник всегда может выбрать такой элемент из оставшихся и такое направление его вращения (по часовой стрелке или против), что этот третий элемент «победит» первые два — будет вращаться быстрее них. Более того, в 75% случаев третий участник может управлять распределением оставшихся «призовых мест» — какой из элементов, выбранных двумя первыми игроками, займёт 2-е место по скорости вращения, а какой — 3-е. Захочу — сделаю так, а захочу — этак.
«Сейф» с нетранзитивными шестернями. Вторая головоломка О. ван Девентера («Haunted Vault») намного сложнее. Это что-то вроде сейфа с четырьмя наружными рукоятками и прорезями над ними, в которых появляются числа, написанные на внутренних дисках. Внутри корпуса десять скрытых шестерён и девять храповиков. Каждая рукоятка сложным, нетранзитивным образом связана сразу с несколькими дисками. Задача: вращая рукоятки, сделать так, чтобы в прорезях над ними появились заданные числа (как при открытии сейфа).

Головоломка Оскара ван Девентера «Haunted Vault». Кадры из видео на интернет-странице https://www.youtube.com/watch?v=MFCH3QmKKdU.
Парадокс нетранзитивного голосования. Если присмотреться ко всем этим конструкциям, можно заметить, что в их основе лежит следующая общая схема.
Возьмём, например, нетранзитивных мартышек. Элемент X — это голова игрушечной мартышки, Y — ложка. В фигурных конструкциях с фломастерами элемент X — это фломастер, Y — углубление в конструкции. Для конструкций с шестернями: X — это бóльшая шестерня, Y — меньшая. Как эта схема (с небольшими изменениями) реализована в гребёнках с клиньями, читатель может рассмотреть сам.
Это очень напоминает структуру нетранзитивного голосования трёх избирателей за трёх кандидатов в парадоксе маркиза де Кондорсе (позднее переоткрытом Льюисом Кэрроллом, автором «Алисы в Стране чудес»).
Есть три избирателя: 1, 2, 3. Каждый из них на выборах ранжирует трёх кандидатов (А, В, С) следующим образом в порядке предпочтительности:
избиратель 1 ранжирует кандидатов в порядке А, В, С;
избиратель 2 ранжирует кандидатов в порядке С, А, В;
избиратель 3 ранжирует кандидатов в порядке B, C, A.
Получается, что:
большинство избирателей (два из трёх — первый и второй) считают, что А лучше В (ставят А перед В);
большинство избирателей (два из трёх — первый и третий) считают, что В лучше С (ставят В перед С);
большинство избирателей (два из трёх — второй и третий) считают, что С лучше А (ставят С перед А).
Итак, кандидат А побеждает кандидата В, В — С, а С — А (как в игре «Камень, ножницы, бумага»).

На этом фото руки образуют два первых столбца «кондорсеподобной» последовательности. Фото Евгения Дубинчука/Фотобанк Лори.
Этому парадоксу посвящено очень много научной литературы, поскольку он связан с доказательством невозможности идеальной, совершенной избирательной системы. Доказательство провёл лауреат Нобелевской премии по экономике Кеннет Эрроу (но это отдельная тема).
Посмотрим на строчки записи парадокса Кондорсе. Последняя буква в каждом ряду переходит в следующем ряду на первое место, смещая две оставшиеся буквы вправо без изменения их порядка. Поглядим на общую схему нетранзитивных механизмов и убедимся, что там происходит то же самое.
Итак, все представленные выше нетранзитивные механизмы построены, можно сказать, как «кондорсеподобные» конструкции. Они предположительно могут стать интерактивными экспонатами какого-нибудь научно-технического музея или школьного физического кабинета. А придумывание нетранзитивных механизмов и машин может оказаться увлекательным делом для заинтересовавшегося любителя механики и геометрии.
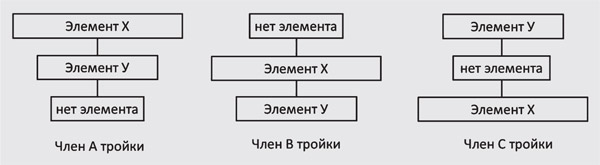
Общая схема, лежащая в основе конструкций, описанных в статье.
Можно ли построить нетранзитивные механически взаимодействующие конструкции по какому-то другому принципу — не по принципу парадокса Кондорсе? Скажем, на основе использования нетранзитивных наборов чисел (вспомним о нетранзитивных кубиках) как геометрических и механических параметров? Или ещё как-то по-другому? Это мне неизвестно и может стать темой отдельного исследования.
Нетранзитивные «красильщики» и клеточный автомат. Придумав вышеописанные конструкции с фломастерами («помечальщиков»), я задался вопросом, что будет, если ситуация усложнится. Представим, что при касании эти конструкции окрашивают одна другую в свой цвет по тому же правилу. Окрашенная, «превращённая в свою» конструкция начинает делать то же самое по отношению к третьей, если касается её, и т. д. Назовём эти конструкции красильщиками.
Пусть у нас есть квадратное поле, состоящее из 3600 ячеек (60 х 60). На нём случайным образом расставлены небольшие кластеры красильщиков 9 возможных цветов. Размер кластера 3 х 3. Кластеры заполняют поле целиком, всего на поле 400 кластеров.
На первом шаге все красильщики осматриваются вокруг себя и делают следующее.
Каждый красильщик 1-го цвета осматривается вокруг себя и, если обнаруживает красильщика 2-го цвета, сосед-ствующего с ним (касающегося стороной или углом), окрашивает его в свой цвет. Соседей другого цвета не окрашивает.
Каждый красильщик 2-го цвета осматривается вокруг себя и, если обнаруживает красильщика 3-го цвета, соседствующего с ним, окрашивает его в свой цвет. Соседей другого цвета не окрашивает.
Каждый красильщик 3-го цвета осматривается вокруг себя и, если обнаруживает красильщика 4-го цвета, соседствующего с ним, окрашивает его в свой цвет. Соседей другого цвета не окрашивает. И т. д.
Правило «окрашиваю соседа, у которого цвет с номером, бóльшим на единицу», действует до красильщиков 9-го цвета. А вот каждый красильщик 9-го цвета осматривается вокруг себя и, если обнаруживает соседа — красильщика 1-го цвета, окрашивает его в свой цвет. Получается, что красильщики красят друг друга по принципу «камень, ножницы, бумага», только типов красильщиков 9, а не 3.
Окрашенный сосед сам пока никого не окрашивает.
На втором шаге процедура повторяется на всём поле. На третьем шаге — снова и т. д.
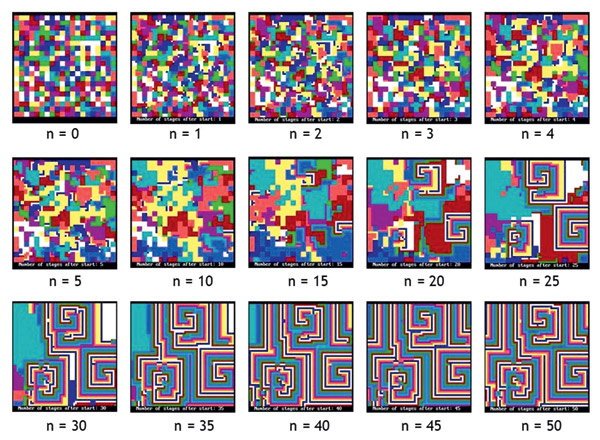
Клеточный автомат: красильщики девяти цветов окрашивают друг друга по правилу нетранзитивной конкуренции на поле 60 х 60. Показана динамика меняющихся цветов.
Я написал компьютерную программу, показывающую, как меняется ситуация на поле на каждом следующем шаге. Посмотрите, что получилось. Показаны исходная позиция со случайным распределением кластеров и позиции на шагах №№ 1, 2, 3, 4, 5, 10, 15, 20, 25, 35, 40, 45, 50. Далее возникшая на поле геометрия не меняется, по ней лишь пробегают цвета на каждом следующем шаге.
То, что мы видим, называется клеточным автоматом, демонстрирующим «возникновение порядка из хаоса». Клеточные автоматы бывают очень разные, с их помощью моделируют химические, биологические, социальные процессы и явления. «Возьмите простое решётчатое пространство. Задайте набор нехитрых правил. Запустите время. Вы получили клеточный автомат — почти что целый мир», — пишет Роман Фишман в научно-популярной статье «Клеточный автомат: возможна ли автоматическая жизнь?» («Популярная механика», 2016, № 3). Ещё один хороший научно-популярный текст: Кац Д. «От эдемского сада до лесных пожаров. Как исследовать мир при помощи клеточных автоматов» («Нож», 28 ноября 2020).
В нашем случае клеточный автомат моделирует отношения нетранзитивной конкуренции, широко изучаемой в биологии.
Как видим, нетранзитивные механические игрушки, интересные и сами по себе, могут служить моделями, связанными как с биологическими, так и с социальными процессами и явлениями — нетранзитивной конкуренции и парадоксами голосования. А может быть, и с моделями ещё чего-то важного — надо подумать.
Рисунки и фото автора.
Комментарии к статье
* Помимо статей, указанных выше, из недавних публикаций о таких кубиках можно упомянуть научно-популярную книгу: Шейнерман Э. Путеводитель для влюблённых в математику. Глава 19. Нетранзитивные игральные кости. — М.: Альпина нон-фикшн, 2018.




