Обезьянки, в отличие от всего остального, там представленного, были всего лишь нарисованы. И я решил, что хорошо бы, чтобы какие-то механические игрушечные обезьянки реально чистили друг другу свои игрушечные зубки по такой же схеме. Обратился к Юрию Иванову из Чистополя, автору деревянных миниатюрных художественных скульптур, который делает и механические куклы. Он счёл задачу интересной, придумал художественное и техническое решение и изготовил эти игрушки. Получилось, по-моему, красиво (см. фото).
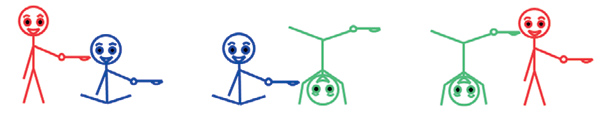
Рукоятки в подставках можно вращать. При этом благодаря системе механической передачи (на заднем плане видны соединительные реечки) начинают качаться вверх-вниз руки с зубными щётками, расположенными как раз на уровне мордочки следующей обезьянки. Можно видеть, что при таком взаимном расположении рук со щётками и мордочек чистка зубов происходит по воображаемому кругу: красная чистит зубки синей, синяя — зелёной, зелёная — красной (как в игре «камень, ножницы, бумага», только здесь не «битье по кругу», а помощь). В математике такие закольцованные структуры отношений называют нетранзитивными циклами.

Механические игрушечные обезьянки, сделанные Юрием Ивановым. Видео работы обезьянок можно посмотреть здесь: https://youtu.be/rRKv90Uj3xM.
А теперь обратимся к нетранзитивным игральным кубикам, про которые я писал ранее в статье «Правило транзитивности против нетранзитивности выбора» (см. «Наука и жизнь» № 3, 2017 г.).
Существуют разные наборы специально сконструированных игральных кубиков. Числа на их гранях — нестандартные. Они рассчитаны так, что кубик А чаще выигрывает у кубика В (показывает большее число на верхней грани), чем проигрывает ему; кубик В чаще выигрывает у С, а С — у A. Числа видны всем игрокам, но чтобы понять закономерности побед и поражений кубиков при попарных многократных бросаниях, нужно знать основы теории вероятности. Посмотрим на один из вариантов таких кубиков с числами из магического квадрата Мартина Гарднера*.
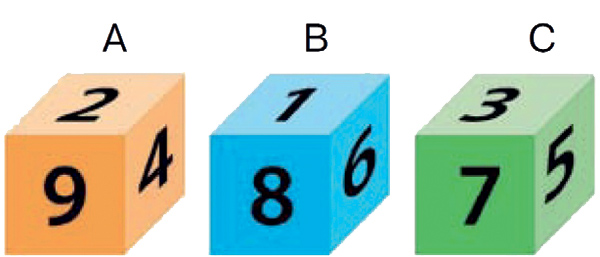
Три кости A, B, C имеют на своих гранях следующие числа:
A: 2, 2, 4, 4, 9, 9
B: 1, 1, 6, 6, 8, 8
C: 3, 3, 5, 5, 7, 7
Вероятность выигрыша кубика А у кубика В — 5/9, B у С — 5/9, С у А — 5/9.
И вот вопрос: чем отличаются циклы нетранзитивных обезьянок и циклы нетранзитивных игральных кубиков (помимо внешнего вида и того, что обезьянок бросать не рекомендуется, они работают по-другому, а кубики как раз надо)?
Обезьянки и кубики образуют нетранзитивные циклы двух разных типов.
Обезьянки образуют цикл того же типа, что элементы нетранзитивного голосования трёх избирателей за трёх кандидатов в парадоксе маркиза де Кондорсе. Об этом парадоксе написано в упомянутой выше статье «Принцип ”камень, ножницы, бумага” в механических игрушках и его ”родственные связи”». И там отмечено, что в записи строчками парадокса Кондорсе последняя буква в каждом ряду, обозначающая тот или иной элемент, переходит на первое место в следующем ряду, смещая две оставшиеся буквы вправо без изменения их порядка. Буква С из конца первой строчки переходит в начало второй, смещая буквы АВ вправо; В из конца второй строчки переходит в начало третьей, смещая СА вправо.
АВС
САВ
ВСА
Здесь А — мордочка игрушечной обезьянки, С — двигающаяся рука со щёткой, В — пространство, где нет ни головы, ни руки со щёткой.
Такой порядок элементов в строчках, который основан на алфавите (А, В, С) и его преобразованиях, называется лексическим, или лексикографическим. Здесь не идёт речь о количественных сравнениях.

Если обозначить зубастую мордочку обезьянки как элемент А, то можно видеть, что он словно смещается от обезьянки к обезьянке по той же диагонали, что и буква А в трёх строчках записи слева внизу. На четвёртой фигурке (она же первая) цикл начинается снова.
А нетранзитивные игральные кубики построены на основе количественных (статистических) закономерностей и сравнений. Различаются и алгоритмы генерации нетранзитивных стохастических объектов типа игральных костей с N сторонами и кондорсеподобных структур нетранзитивных механических объектов.
При этом и у тех и у других есть сущностные сходства — например, можно строить сколь угодно длинные цепочки объектов обоих типов.
Напоследок отмечу, что в программировании есть процедура «цикл в цикле» («вложенные циклы»). Внутрь первого цикла перебора вложено сколько-то циклов перебора нижележащего уровня, внутри каждого из них — сколько-то циклов следующего уровня и т. д. Для объектов обоих типов тоже возможны нетранзитивные циклы внутри нетранзитивных циклов — причём в неограниченном количестве уровней погружения. Мы с доктором физико-математических наук А. В. Лебедевым с механико-математического факультета МГУ им. М. В. Ломоносова занялись изучением их свойств. О результатах расскажем позже.
Рисунки и фото автора.
Комментарии к статье
* Гарднер М. Путешествие во времени. — М.: Мир, 1990, с. 71.




