ЕСТЬ ЛИ «ЦАРСКАЯ ДОРОГА» В МАТЕМАТИКЕ?

Те, кто изучал математику, наверное, помнят о Евклиде (в греческом написании — Eυκλειδης) — авторе фундаментального труда «Начала», в 15 книгах которого изложены аксиоматические основы геометрии (две книги, посвященные многогранникам, иногда приписывают Гипсилу Александрийскому). Предание гласит, что египетский правитель Птолемей I Сотер посетил мыслителя и поинтересовался, существует ли более короткий способ познания геометрии, чем тот, который изложен в «Началах». Ответ древнего мыслителя: «В науке нет царской дороги» — приводят как блестящий аргумент в пользу необходимости приложить немало усилий, чтобы освоить математику или любую другую науку.

А разве говорил великий Евклид, что изучение науки должно быть скучным? Конечно, нет. Но на практике получается, что многие предметы, в том числе и математика, ученикам кажутся неинтересными. Почему многие помнят историю про Евклида, а вот что такое логарифм, могут сформулировать с большим трудом? И стоит ли винить в этом нерадивых учеников, среди которых не то что царей, но и царских потомков малая доля?

В 1884 году увидела свет замечательная книга англичанина Эдвина Эббота «Флатландия» («Flatland» ), в увлекательной форме рассказавшая о многомерных пространствах. И хотя книга не предлагала «царского пути» в геометрии, она позволяла преодолеть эту дорогу с большими удобствами, чем классические учебники. Вместо того чтобы формулировать теоремы и потом приводить их доказательства, автор создал образ необычной страны, обитатели которой не ведают о трехмерном пространстве так же, как нам не дано увидеть четырехмерный мир. Описание этого необычного государства занимает намного больше места, чем простая фраза вроде того, что «...в четырехмерном пространстве координаты точки задаются четырьмя числовыми значениями». Но зато у читателя появляется наглядное представление о том, как можно изучать четырехмерные пространства. Подчеркиваю, не наблюдать, а изучать. А когда такое представление получено, легче воспринять математический аппарат, который используется в строгом описании многомерных пространств.

СТРОГО, НО НЕПОНЯТНО

Наглядный подход облегчает понимание и других специальных понятий. В математике принято облекать в строгую абстрактную форму довольно простые вещи, которые можно объяснить «на пальцах» даже школьнику начальных классов. К сожалению, то, что просто показать, не всегда легко доказать. В доказательствах не обойтись без развитого и сложного математического аппарата. Так, классическое определение непрерывной функции в математическом анализе выглядит не таким уж и легким:

Функция f(х) является непрерывной в точке х₀, если:

1. Она определена в точке х₀ и некоторой окрестности этой точки.

2. Для любого числа ε > 0 можно указать такое число δ > 0, зависящее от е, что для всякого х, удовлетворяющего неравенству |х - х₀| < δ, следует, что |f(x) — f(х0)| < ε.

Функция, непрерывная в каждой точке отрезка (интервала, полуинтервала и т.д.), называется непрерывной на этом отрезке (интервале, полуинтервале и т.д.).

Намного проще объяснить понятие непрерывной функции с помощью листа бумаги и карандаша. Достаточно нарисовать два графика: один — с непрерывной линией, другой — с точкой разрыва.

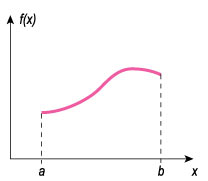
График гладкой непрерывной функции на отрезке [a, b].

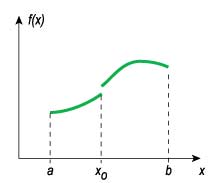
График функции, имеющей разрыв в точке х₀ отрезка [a, b].

Такой рисунок сразу позволяет понять: непрерывная функция потому и непрерывная, что ее график можно нарисовать одной линией, ни разу не отрывая карандаша от бумаги. Интересно, насколько меньше стало бы «хвостатых» студентов, если бы преподаватели уделяли часть времени наглядной подаче материала?

Возьмем другой пример — теорему Вейерштрасса. Она гласит:

Любая, непрерывная на отрезке функция является ограниченной и достигает на нем своего максимума и минимума.

Довольно очевидное утверждение, если подходить к нему с практических позиций. После одной-двух минут размышления любой студент скажет, что нарисовать график функции неограниченной и непрерывной на отрезке невозможно.

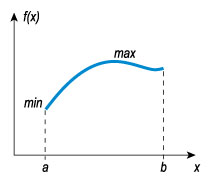
У непрерывной на отрезке функции всегда найдется минимум и максимум.

Но чтобы строго доказать это, нужно повторить ход рассуждений Карла Вейерштрасса — «отца» современного математического анализа.

Страдает отсутствием наглядности и классическое определение дифференцируемой, или, проще говоря, гладкой функции:

Функция f(х), определенная в некоторой окрестности точки х₀, называется дифференцируемой в точке х₀, если может быть представлена в виде

f(х)= f(х0) + C (х -х0) + о(x - х₀),

где C — константа;

о(x - х₀) — функция, пренебрежимо малая в сравнении с величиной (x - х₀).

После такого определения быстренько доказывают теорему о том, что если функция дифференцируема в точке х₀, то она имеет в этой точке конечную производную. Ну а затем объявляют функцию f(х) гладкой на интервале, если она дифференцируема в каждой точке этого интервала.

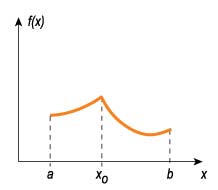
График функции, не дифференцируемой в точке х₀.

Казалось бы, чего проще, нарисовать картинку с функцией, график которой имеет излом, а потом уже предложить вниманию учащихся строгое математическое определение? Но как раз на наглядное изложение материала времени в учебной программе обычно не предусмотрено.

Попробуйте нарисовать гладкую кривую, которая на концах отрезка принимает равные значения, но так, чтобы у нее не было точки, касательная к которой параллельна оси абсцисс. Не получается? Еще бы, такой кривой попросту не существует. Убедиться в этом с карандашом в руках может каждый. Но строгое доказательство приведено в теореме французского математика Мишеля Ролля (1652—1719):

Если функция, непрерывная на отрезке [a, b] и дифференцируемая внутри него, принимает на концах равные значения, то ее производная по крайней мере один раз обратится в ноль на интервале (a, b).

А ведь после математического анализа, где поначалу изучают функции одной переменной, переходят к функциям многих переменных. Там понятия непрерывности и гладкости тоже вводятся в виде строгих математических определений, но наглядности от этого не прибавляется.

ПРОЩЕ ПРЯМОЙ ТОЛЬКО ТОЧКА

Страдает отсутствием наглядности и такой раздел математики, как линейная алгебра. После долгого изучения различных понятий и свойств матриц студенты обычно переходят к решению систем линейных уравнений вида

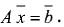
В этом уравнении 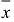— n-мерный вектор-столбец, b— m-мерный вектор-столбец, A — матрица размером m х n. Наглядный пример мог бы сильно помочь студентам в изучении линейной алгебры. Для этого достаточно взглянуть, как выглядит графическая интерпретация системы линейных уравнений с двумя неизвестными на плоскости. Уравнение прямой на плоскости имеет вид

ax + bx = c.

(Те, кто не любит букв, могут вместо a, b и c подставить какие-нибудь числа.)

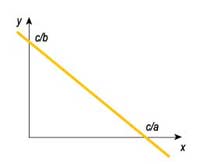
Геометрическая интерпретация уравнения ax + by = c

Две прямые на плоскости описываются двумя линейными уравнениями:

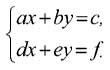
Любой, даже далекий от математики человек догадывается, что две прямые на плоскости либо пересекаются, либо параллельны, либо просто совпадают. В первом, наиболее типичном случае точка пересечения двух прямых будет единственным решением системы линейных уравнений.

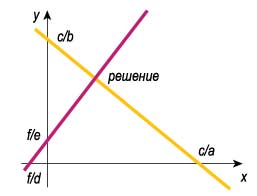
Координаты точки пересечения прямых будут решением системы двух линейных уравнений с двумя неизвестными.

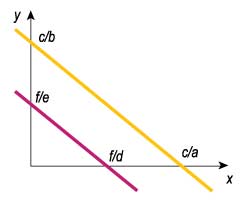
Если прямые не пересекаются, значит, система линейных уравнений не имеет решений.

Когда две прямые параллельны — общих точек нет, и тогда система линейных уравнений решений не имеет. Ну а если две прямые совпадают, то у системы бесчисленное множество решений. Но геометрическая интерпретация хороша только тогда, когда надо понять, что такое система линейных уравнений. А вот чтобы находить эти решения, как раз и нужна строгая математика. Две прямые параллельны, если их уравнения можно представить в виде

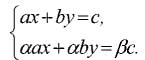
Проще говоря, прямые параллельны (решения нет), если коэффициенты при неизвестных х и y пропорциональны. Если при этом еще и свободные члены пропорциональны, то вторая прямая попросту совпадает с первой (решений бесчисленное множество).

Кто бы мог подумать, что мы почти объяснили, о чем идет речь в теореме Кронекера — Капелли:

Система линейных уравнений имеет хотя бы одно решение тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Напомним, что расширенная матрица — это матрица системы, к которой добавили столбец, составленный из свободных членов, стоящих в правой части системы уравнений.

Когда прямые параллельны, т.е. коэффициенты при неизвестных пропорциональны, а свободные члены — нет, ранг матрицы системы равен 1, а вот ранг расширенной матрицы — 2.

ОТ ДВУХ ИЗМЕРЕНИЙ — К ТРЕМ

Для системы из трех линейных уравнений с тремя неизвестными ситуация немного сложнее. Одно линейное уравнение соответствует плоскости в трехмерном пространстве:

ax + bx + cz = d.

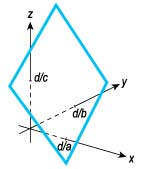
Геометрическая интерпретация уравнения

Система трех линейных уравнений также может иметь одно решение, не иметь решений или иметь бесчисленное множество решений.

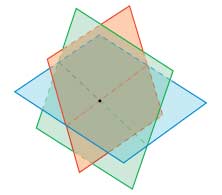
Координаты точки пересечения трех плоскостей будут решением системы трех линейных уравнений с тремя неизвестными.

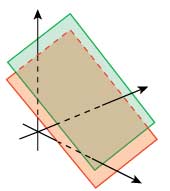
Решений нет, когда две плоскости из трех параллельны.

Ситуация, при которой решений нет, потому что две плоскости из трех параллельны, аналогична параллельным прямым на плоскости. Но в трехмерном пространстве решения может не быть еще из-за того, что прямая, образованная пересечением двух плоскостей, параллельна третьей плоскости.

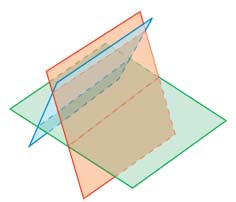
Решений нет, когда прямая — пересечение двух плоскостей — параллельна третьей плоскости.

Теорема Кронекера — Капелли хотя и не является столь наглядной, как геометрические рисунки, зато предлагает очень удобный механизм, позволяющий вычислить, имеет система решения или нет.

От систем линейных уравнений перейдем к системам линейных однородных уравнений. Это такие системы, у которых свободные члены равны 0. В трехмерном пространстве каждое уравнение такой системы будет задавать плоскость, которая проходит через точку — начало координат. Понятно, что однородная система всегда имеет по крайней мере одно, нулевое, решение. Рассмотрим систему двух линейных уравнений с тремя неизвестными:

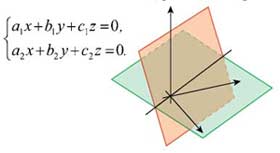
Координаты любой точки, лежащей на пересечении двух плоскостей, будут решением однородной системы двух уравнений с тремя неизвестными.

Если коэффициенты такой системы непропорциональны (в переводе на геометрический язык — плоскости совпадают), то две плоскости пересекаются. В таком случае решением системы будут точки прямой, образованной пересечением двух плоскостей. Размерность решения — 1. А ранг системы — 2. Обратите внимание, что 2 + 1 = 3 — количество неизвестных. Этот пример служит наглядным подтверждением известной теоремы:

Размерность пространства решений системы однородных линейных уравнений с n неизвестными равна n-r, где r — ранг матрицы системы.

ЛИНЕЙНО ПОПРОГРАММИРУЕМ

Переходя от уравнений к неравенствам, изобразим полуплоскость — множество точек, координаты которых удовлетворяют условиям

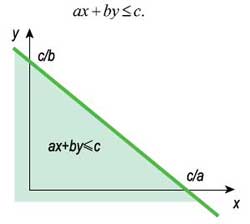
Геометрическая интерпретация неравенства ax + by = ≤c.

Системы линейных неравенств в геометрической интерпретации могут описывать довольно сложные множества точек на плоскости. Пересечение нескольких полуплоскостей образует выпуклые многоугольники, которые задают множество точек, удовлетворяющих нескольким линейным неравенствам:

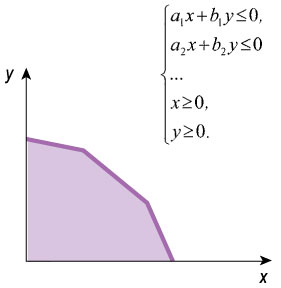
Система линейных неравенств с двумя неизвестными в геометрической интерпретации зачастую представляет выпуклый многоугольник.

В линейном программировании занимаются изучением задачи поиска максимума линейной функции на множестве, образованном линейными неравенствами. Линейная функция, максимум которой ищут, в случае двух переменных выглядит следующим образом:

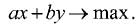
Если рассмотреть набор параллельных прямых, заданных уравнениями:

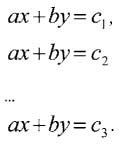
в которых значение свободного члена увеличивается (то есть с₁ < с₂ < ... < с₃), то из рисунка будет понятно, что максимум целевой функции достигается либо в вершине многогранника условий, либо на его стороне.

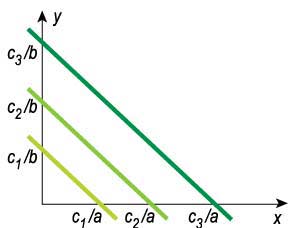
С ростом значения свободного члена прямые «удаляются» от начала координат.

В первом случае решение задачи линейного программирования будет единственным. Когда максимум целевой функции достигается в любой точке стороны выпуклого многоугольника, задача имеет бесчисленное множество решений. В этом случае у многоугольника целых две вершины будут решением исходной задачи.

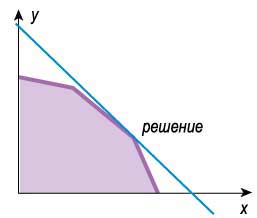
На одной из вершин будет достигнут максимум целевой функции.

Отсюда можно сделать вывод, что одна из вершин многоугольника условий является решением задачи линейного программирования. К такому выводу и приходит одна из основных теорем линейного программирования:

Если существует решение задачи линейного программирования, то оно достигается в одной из угловых точек множества допустимых решений.

В трехмерном пространстве множество условий часто представимо в виде выпуклого многогранника. Целевая функция может достигать своего максимума как в вершине, так и на ребре или даже на целой грани многогранника. Но главный вывод остается неизменным: одна из вершин является решением задачи.

Геометрический способ поиска максимума целевой функции напрашивается сам собой: давайте попробуем последовательно перебрать все вершины многогранника условий. Одна из них и будет являться решением. Возможно, кого-то удивит, что знаменитый симплекс-метод как раз и занимается перебором угловых точек — вершин. Именно этот способ зачастую эффективно используется при обработке многих экономических моделей, сводящихся к задачам линейного программирования.

О ФОРМАХ... КВАДРАТИЧНЫХ

При изучении высшей алгебры студенты занимаются изучением квадратичных форм n переменных. От выражения, которое предстоит изучать, холодеет в груди:

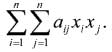
В матричном виде представление этого «монстра» несколько проще, но наглядности не добавляет:

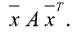
Здесь 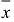= (х₁, х₂ ..., х_n) — вектор-строка, А — симметричная матрица. Интересно, что в случае двух переменных квадратичная форма имеет вид

a₁₁x₁² + 2a₁₂x₁x₂ + a₂₂x₂².

Если рассмотреть набор точек, который удовлетворяет равенству

a₁₁x₁² + 2a₁₂x₁x₂ + a₂₂x₂² = 1,

то это будет кривая второго порядка: эллипс, парабола или гипербола, в зависимости от значений коэффициентов квадратичной формы.

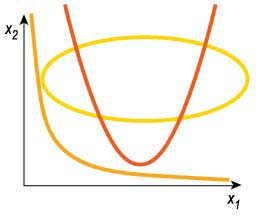
Квадратичная форма на плоскости — это кривая второго порядка.

В случае эллипса можно подобрать систему координат так, чтобы ее начало располагалось в центре эллипса, а оси координат были направлены по его главным осям. Для перехода к «удобной» системе координат потребуется перенести ее начало и повернуть на некоторый угол координатные оси (такие преобразования относятся к линейным).

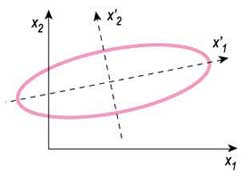
Иметь дело с эллипсом намного удобнее в системе координат, центр которой совпадает с началом координат, а координатные оси направлены по главным осям.

В «удобной» системе координат уравнение кривой второго порядка станет намного проще. Для эллипса оно будет выглядеть так:

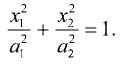
Такое уравнение эллипса называется каноническим. Размеры полуосей эллипса равны а₁ и а₂. По сути, каноническое уравнение кривой второго порядка — частный случай квадратичной формы, матрица которой имеет диагональный вид:

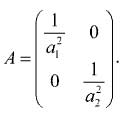
Сравните полученный результат с известной теоремой:

Любую квадратичную форму можно с помощью невырожденного линейного преобразования привести к каноническому (или диагональному) виду.

В заключение я хотел бы принести извинения за нестрогость многих рассуждений. Главной целью статьи была наглядность. Думаю, что существует множество других интересных примеров, которые помогли бы преодолению совсем не «царской» дороги в математике. Автор будет признателен всем, кто сможет предложить свои примеры наглядного и доходчивого объяснения математических понятий.

Подробности для любознательных

О ЧЕТВЕРТОМ ИЗМЕРЕНИИ — ДОСТУПНО

Автор “Флатландии” англичанин Эдвин Эббот (Edwin Abbott) был школьным учителем. Родился он 10 декабря 1838 года, умер 12 октября 1926 года. Образование получил в Кембриджском университете. Занимаясь изучением и преподаванием математики и теологии, он написал несколько книг, но самой популярной стала вышедшая в 1884 году “Flatland”. В ней Эббот смог не только познакомить читателя с удивительной плоской страной, которую населяли геометрические фигуры. Ему удалось с легкой иронией передать атмосферу и модные воззрения своего времени.

Форма изложения оказалась настолько удачной, что спустя почти 70 лет датский математик Дионис Бюргер (Dionijs Burger) решил использовать ее для создания продолжения и написал не менее увлекательную “Сферландию” (“Bolland”). В 1957 году книга увидела свет, а в1965 году была издана на английском языке под названием “Sphereland”.

Популярность двухмерной страны оказалась столь высокой, что в 1965 году в Гарвардском университете был создан 11-минутный мультфильм о жизни геометрических фигур. Созданием ленты руководил художник Эрик Мартин (Eric Martin). Вторую попытку экранизировать “Флатландию” предпринял итальянский математик Мишель Эммер (Michele Emmer), который выпустил 22-минутный мультфильм.

В XXI веке появилось уже несколько проектов, в которых герои Флатландии предстают на экранах. В 30-минутной ленте, созданной специалистами Flat World Productions LLC в 2006 году, можно воочию увидеть, как живут герои Эдвина Эббота.

Самый крупный проект о двухмерной стране принадлежит корпорации Flatland Production Corp. В 2007 году под управлением Лэда Элингера (Ladd Ehlinger Jr) создан 95-минутный мультфильм о приключениях геометрических фигур. Жизнь рисованных героев: треугольников, квадратов, сфер и других — на удивление напоминает наши будни, с той только разницей, что мы воспринимаем на одно измерение больше. Так же, как и у нас, у жителей Флатландии бьется сердце, течет по жилам кровь, только все это происходит на плоскости. И хотя рисованные герои совсем не похожи на людей, что-то человеческое в них все-таки есть.

На русском языке “Флатландия” и “Сферландия” впервые были изданы в 1976 году издательством “Мир”. Автор перевода — Юлий Александрович Данилов (1936—2003), профессор, ведущий научный сотрудник Российского научного центра “Курчатовский институт”. В его переводе в нашей стране выходили также популярные книги по математике Мартина Гарднера (“Математические новеллы”, “Математические досуги”, “Математические головоломки и развлечения” и другие), которые хорошо знакомы любителям математики. За перевод книг американского физика-теоретика Георгия Гамова о мистере Томпкинсе Данилов получил в 1994 году премию и медаль имени Александра Беляева, присуждаемые за достижения в области научной фантастики.

Подробности для любознательных

РАНГ БЕЗ ТАБЕЛЯ

Понятие ранга матрицы тоже поддается наглядному объяснению. Для этого стоит напомнить, что вектор, координаты которого (a, b) составлены из коэффициентов в уравнении прямой ax + by = c, будет перпендикулярен ей. Обычно строгому доказательству этого факта посвящают целую теорему, но на плоскости это понятно из рисунка.

Для системы двух линейных уравнений с двумя неизвестными строки матрицы образуют два вектора нормалей. Если прямые, соответствующие уравнениям системы, параллельны, то векторы нормалей окажутся на одной прямой (размерность прямой 1). Такую пару векторов называют линейно зависимой.

Для системы из трех линейных уравнений с тремя неизвестными векторы нормалей будут располагаться в трехмерном пространстве. Они линейно зависимы, если лежат вдоль одной прямой (размерность 1), или в одной плоскости (размерность 2).

Строгое определение линейной зависимости менее наглядно:

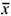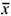Векторы ₁, ₂ ...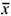_n называют линейно зависимыми, если существуют коэффициенты α₁, α₂ ...α_n, не все равные нулю (то есть α₁² + α₂² + ... + α_n² ≠ 0), такие, что α₁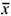₁ + α₂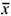₂+ ...+ α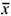_nn= 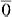. Если это равенство выполняется только при α₁= α₂ = ...= α_n = 0, то система векторов называется линейно независимой.

Ранг матрицы системы линейных уравнений совпадает с размерностью множества, в котором располагаются векторы нормалей. Если все векторы нормалей направлены вдоль прямой, ранг матрицы — 1, если они лежат в плоскости, ранг равен 2. Классическое определение значительно строже, но его наглядность намного ниже:

Ранг матрицы — наивысший из порядков, отличных от нуля миноров этой матрицы.