Интерференция — замечательное явление, имеющее множество применений. Оно прояв-Лж. ляется как в оптическом, так и в радиодиапазоне. Особенно впечатляюща интерференция света, так как мы можем её наблюдать непосредственно, в то время как радиоволны невидимы глазом. Часто интерференцию света характеризуют такой «парадоксальной» фразой: свет плюс свет может давать темноту. Человеку, совершенно незнакомому с физической оптикой, это может показаться очень странным: как это так — если к свету прибавить ещё свет, то должно стать ещё светлее! Правда, все мы изучали физику в школе, и, наверное, всё-таки у каждого остались хотя бы какие-то смутные воспоминания о том, что такое интерференция («Да... что-то связанное со светом... не очень помню, но вроде бы это какое-то наложение световых волн...»). Уже хорошо! Давайте же начнём с того, что освежим эти полузабытые знания, которые позволят нам побеседовать о крайне удивительных и интересных явлениях, связанных с интерференцией света.
Возьмём более или менее «направленный» источник света, например карманный фонарик (с галогенной лампочкой, дающей яркий свет, а ещё лучше — со светодиодом), и направим его на белый экран. На экране возникнет пятно света. Теперь возьмём второй такой же фонарик и направим его свет на то же место экрана. «И что, мы получим темноту?» — иронически спросит читатель, прочитавший преды-дущий абзац, но настолько позабывший школьную физику, что слово «оптика» ассоциируется у него лишь с очками и лупами. Нет, конечно, никакой темноты мы не получим, световое пятно станет ещё ярче. «Ну и что в этом удивительного?» — заметит наш скептик. В этом — ничего. Но теперь сделаем следующее: возьмём лист плотного картона, проколем в нём иголкой две дырочки как можно ближе одну к другой (скажем, на расстоянии 0,5 миллиметра), поставим лист перед экраном (на расстоянии около 20—30 см) и осветим эти дырочки одним фонариком (см. рис. 1). Возможно, придётся немного порегулировать расстояние между фонариком и картоном, но мы обязательно найдём положение, при котором на экране светлое пятно будет пересекаться тёмными участками. Вот мы и получили темноту!
Почему же возникают эти тёмные участки? Почему их не было в случае двух фонариков, а появились они только при освещении отверстий в картоне одним фонариком?
Зададим такой «нелепый» вопрос. Сколько источников света было в этих двух случаях? Я назвал этот вопрос «нелепым» потому, что он может вызвать недоумение: как сколько? В первом случае мы включали оба фонарика, значит, было два источника света, а во втором светил только один фонарик, один источник света. Разве не так?
Нет, не так. Во втором случае было тоже два источника, которыми стали два отверстия в картоне (1 и 2, рис.1). То есть исходный источник был, конечно, один, но свет на экран шёл из этих двух дырочек, которые играли роль вторичных источников света. А вот то, что свет этих вторичных источников образовался от одного исходного, сыграло фундаментальную роль.
Используя картон с дырочками, изображённый на рис.1, мы воспроизвели (с некоторыми несущественными отличиями) знаменитый опыт Т. Юнга, впервые наблюдавшего интерференцию света от двух щелей в 1802 году.
Интерференция — это такое сложение волн, при котором происходит не просто суммирование интенсивностей этих волн, а их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от разности фаз волн в этих точках.
Но прежде чем рассматривать интерференцию, необходимо поговорить об одном фундаментальном понятии, играющем ключевую роль.
Почему в случае с двумя фонариками происходило только суммирование интенсивностей (яркостей), а в случае с картоном мы могли наблюдать интерференцию? Потому, что в первом случае световые волны от двух источников были некогерентны, а во втором — когерентны, так как порождены одним источником. Следовательно, необходимым условием образования интерференции является когерентность волн. Что это такое?
Слово «когерентность» — греческого происхождения и в наиболее общем смысле означает «согласованность». Простейший пример: когда по улице прогуливается толпа людей, она идёт некогерентно, а когда марширует рота солдат, то она идёт когерентно.
Когерентные волны — это волны одинаковой частоты, между которыми сохраняется постоянная разность фаз (то есть они согласованы по фазе). При сложении двух когерентных волн одинаковой поляризации (с одним и тем же направлением колебаний напряженности электрического поля) амплитуда суммарной волны зависит от разности фаз складываемых волн — это и есть интерференция.
При интерференции световых волн удобнее иметь дело не с амплитудами, а с интенсивностями. Это не меняет существа дела, так как интенсивность пропорциональна квадрату амплитуды. Если в какую-либо точку приходят две волны с интенсивностями I1 и I2 и фазами φ1 и φ2 соответственно, то результирующая интенсивность в этой точке определяется выражением
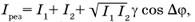
где ∆φ = | φ 1 - φ 2 | — разность фаз, а множитель у отражает степень когерентности волн. Из этой формулы наглядно видна зависимость результирующей интенсивности от разности фаз ∆φ и от величины γ.
В тех местах, куда волны приходят в одинаковой фазе, то есть «гребни» и «впадины» одной волны совпадают с «гребнями» и «впадинами» другой (∆φ =0 , cos ∆φ = 1), волны усиливают одна другую и наблюдается максимальная интенсивность (I max). В тех местах, куда волны приходят в противофазе, «гребни» одной волны совпадают со «впадинами» другой ( ∆φ = 180о, cos ∆φ = —1), волны гасят одна другую и результирующая интенсивность становится минимальной (Imin ). Таким образом, образуется интерференционная картина, состоящая из чередующихся светлых и тёмных участков.
Когерентность волн определяет их способность к интерференции. Практическим критерием степени постоянства разности фаз, то есть мерой степени когерентности у, является контраст (видность, резкость, чёткость) интерференционных полос — важнейший параметр интерференционной картины. Если условие ∆φ = const не соблюдается, то, как видно из вышеприведённой формулы, изменяется и результирующая интенсивность Iрез, что приводит к «размытию» интерференционных полос — уменьшению контраста К. В общем случае контраст определяется выражением
K=(Imax - Imin) / (Imax + Imin).
При этом 0 < К < 1. Крайние значения соответствуют предельным случаям полной некогерентности (К = 0) и полной когерентности (К = 1) волн. Остальные значения соответствуют промежуточным случаям частичной когерентности. Смысл величины у состоит в том, что она дает информацию о контрасте интерференционной картины. Нетрудно показать, что если интенсивности интерферирующих волн равны (I1 = I2 = I), то К = γ, то есть значение γ непосредственно равно величине контраста К.
Теперь, прояснив наиболее существенные моменты, касающиеся интерференции, перейдём к нашей основной теме, сформулированной в заголовке статьи.
Существует множество интерференционных схем (интерферометров), но достаточно рассмотреть только одну из них. Вернёмся к уже знакомой схеме интерферометра Юнга (рис.1). На экране наблюдается интерференционная картина. Будем постепенно уменьшать интенсивность света. Освещённость экрана станет падать, но интерференционная картина сохранится. Продолжим уменьшать интенсивность света, а вместо экрана поставим фотопластинку, потому что глазом уже ничего не видно (рис. 2). Увеличив время экспозиции и проявив пластинку, обнаружим на ней всё ту же интерференционную картину (на рис. 2 это показано кривой D, отображающей интерференционное распределение полос). Уже интересно: значит, интерференция не зависит от интенсивности света? Продолжаем опыт, все больше уменьшая интенсивность и соответственно увеличивая время экспозиции. Короче говоря, при достаточно длительной экспозиции можно обнаружить интерференционную кривую D в принципе при сколь угодно малой интенсивности света. Но с уменьшением интенсивности светового пучка уменьшается число фотонов в нем, и наступит такой момент, когда вместо световых волн в интерферометр Юнга будут поступать отдельные фотоны. Вот излучился один фотон, за ним другой и т.д. — фотоны поступают в интерферометр сугубо поодиночке. Но при этом сохраняется интерференционный характер кривой D, на фотопластинке получается такая же интерференционная картина, как и от световых волн!
Как же это может быть? Ведь для получения интерференции необходимо, чтобы свет поступал на пластинку одновременно от двух отверстий 1 и 2. Но отдельный фотон не может пройти сразу через оба отверстия. Он проходит либо через отверстие 1, либо через отверстие 2. Очевидно также, что он не может разделиться на две «половинки». И вот тут мы сталкиваемся с совершенно мистической ситуацией. Фотон проходит через одно отверстие, но эффект такой, как будто он прошёл через оба. Это приводит к парадоксальному утверждению: нельзя считать, что фотон проходит через одно отверстие независимо от другого. Если бы это было так, то при прохождении, скажем, через отверстие 1 было бы совершенно безразлично, открыто или закрыто отверстие 2. Но если мы закроем отверстие 2, то, как показывает опыт, интерференционная картина немедленно исчезнет!
Всё это очень странно. Более того — непостижимо. Но вернёмся к схеме Юнга — нас ждёт ещё много интересного.
Итак, мы имеем дело с отдельными фотонами. Закроем отверстие 2. Теперь мы точно знаем, что фотоны проходят только через отверстие 1. Интерференция исчезает, и распределение попаданий фотонов на фотопластинку за некоторый достаточно большой интервал времени описывается кривой А (рис. 2). Теперь откроем отверстие 2 и закроем 1. Фотоны будут проходить только через открытое отверстие 2, и их распределение отобразится кривой В. Теперь откроем оба отверстия. Если, как этого требует логика, считать, что каждый фотон проходит либо через одно, либо через другое отверстие, то на фотопластинке-детекторе должна зафиксироваться сумма этих распределений, то есть кривая С (обозначенная на рис. 2 пунктиром). Но возникает не суммарное, а интерференционное распределение D. То есть фотон при прохождении того или другого отверстия каким-то образом «ощущает» соседнее отверстие; в противном случае, как уже говорилось, фотону было бы «безразлично», открыто или закрыто это соседнее отверстие, и при обоих открытых отверстиях должна была бы фиксироваться суммарная кривая С. Это удивительное появление интерференции при прохождении фотонов через одно отверстие - чисто квантовый эффект, один из парадоксов квантовой механики, который невозможно объяснить на основе классической теории.
Но пойдём дальше. Описанный эффект наблюдается не только с фотонами, но и с электронами, протонами, нейтронами, то есть с микрообъектами (подобные эксперименты производились неоднократно). Особенно наглядными были опыты с электронами, которые вроде бы уж точно «частицы», а не волны. И вот физики придумали, как «подглядеть», каким образом электрон проходит через отверстия. Они поместили вблизи каждого отверстия по источнику света и фотоприёмнику, расположив их так, что фотоприёмники регистрируют свет, рассеянный электроном. Если электрон проходит через одно отверстие, сработает один фотоприёмник, и мы узнаем, через какое именно отверстие прошёл электрон; если же он непостижимым образом пройдет сразу через оба отверстия, то сработают оба фотоприемника. Что же дал такой опыт?
Оказалось, что всегда срабатывает только один фотоприёмник и никогда не срабатывают оба одновременно. Значит, электрон всегда проходит только через одно отверстие, и мы всегда можем сказать, через какое именно. Что же получается? Что электрон, проходя через одно отверстие, каким-то образом «ощущает» другое? Но давайте наберём достаточно большое число попаданий электронов на разные места экрана и посмотрим, как распределятся эти попадания. (В случае электронов вместо фотопластинки используется передвижной детектор, например счётчик Гейгера или другое устройство, откликающееся при попадании на него электрона, скажем, щелчком в динамике.) И вот тут обнаруживается совершенно неожиданная вещь. Кривая распределения оказывается не интерференционной, а суммарной! А если мы уберём источники света и фотоприёмники, то получится интерференционная кривая. Другими словами, попытка «подглядеть» за электронами разрушает интерференцию!
Но может быть, освещая электроны, мы изменили их движение? Вполне возможно: ведь фотоны света, сталкиваясь с электронами, оказывают на них какое-то воздействие. Наверное, надо как-то уменьшить это воздействие до практически пренебрегаемого, чтобы интерференционная картина не разрушалась. Но как? Уменьшить интенсивность подсветки? Это ничего не даст, так как при этом будет уменьшаться число фотонов в пучке, и если мы добьёмся испускания света отдельными фотонами, то просто возрастёт количество «незарегистрированных» электронов. Нужно уменьшать не интенсивность, а энергию фотонов. Однако для этого есть только один путь — увеличивать длину волны света или, что то же, уменьшать частоту световых колебаний: энергия фотона (кванта света) Е связана с оптической частотой ν соотношением Е = hν, где h — постоянная Планка. Значит, чем больше длина волны, тем меньше её энергия и тем слабее воздействие на электрон. Самый длинноволновый свет в видимой области — красный; ещё лучше взять инфракрасное излучение, у которого длина волны может быть гораздо больше. Но — увы! — этот путь тоже оказывается тупиковым. Ибо, как только длина волны сравняется с расстоянием между отверстиями, невозможно будет разобрать, возле какого отверстия произошла вспышка. Если длина волны будет намного превышать расстояние между отверстиями — вот тогда возмущение, оказываемое светом, станет настолько слабым, что снова появится интерференционная кривая, но при этом не окажется никакой возможности установить, куда прошёл электрон.
Предпринималось ещё много попыток придумать опыт, который позволил бы «наблюдать» за электронами без разрушения интерференции, но ни одна из них не увенчалась успехом.
Мы рассмотрели эту проблему с чисто качественной стороны, ибо строгое аналитическое рассмотрение требует знакомства с математическим аппаратом квантовой механики. Поэтому ограничимся сказанным, из которого следует вывод: при интерференции отдельных фотонов, электронов и прочих микробъектов любые попытки проследить, как она образуется, немедленно разрушают интерференционную картину. Почему природа не позволяет нам понять механизм подобного явления — на этот вопрос не может ответить никто, по крайней мере в настоящее время. И здесь уместно привести слова выдающегося американского физика Ричарда Фейнмана: «Мы говорим «в настоящее время», но мы очень серьёзно подозреваем, что всё это — уже навсегда и разгрызть этот орешек человеку не по зубам, ибо такова природа вещей».
ПОДРОБНОСТИ ДЛЯ ЛЮБОЗНАТЕЛЬНЫX
Кривые А и В на рис.2 отражают распределение вероятностей попадания микрообъектов (фотонов, электронов) в ту или иную точку вдоль экрана (фотопластинки, детектора). При открытом отверстии 1 и закрытом 2 вероятность описывается кривой А; обозначим эту вероятность Р1. При открытом отверстии 2 и закрытом 1 вероятность описывается аналогичной кривой В; эту вероятность обозначим Р2. Если открыты оба отверстия, то логично ожидать, что результирующая вероятность Р будет суммой вероятностей Р1 и Р2, то есть Р = Р1+ Р2, что соответствует кривой С. Но опыт показывает, что этого не происходит: результирующая вероятность Р соответствует не суммарному, а интерференционному распределению, описываемому кривой D. Вероятность, соответствующую этому распределению, обозначим Р12. Таким образом, при обоих открытых отверстиях получаем Р = Р12 ≠ Р1+ Р2. Как это можно интерпретировать?
В квантовой механике вводят понятие комплексной волновой функции ψ описывающей микрообъект и связанной с вероятностью таким образом, что вероятность есть квадрат модуля (абсолютной величины) волновой функции, то есть | ψ |2. Термин «волновая функция» впоследствии заменили термином «амплитуда вероятности», чтобы подчеркнуть вероятностный характер описания микробъекта. Итак, для нашего случая имеем: Р1 = | ψ 1 |2, Р2 = | ψ 2|2. А далее надо учесть принципиальное обстоятельство, связанное с различимостью взаимоисключающих событий. Что под этим понимается?
У микрообъекта — скажем, у электрона — имеется возможность альтернативной реализации двух вариантов (событий): пройти либо через отверстие 1, либо через отверстие 2. Когда подсветка выключена, то есть мы не наблюдаем за электроном, то эти события являются неразличимыми. Как только мы включаем свет, они становятся различимыми. Ничего подобного нет в классической физике (там все события всегда различимы), такая ситуация возможна только в микромире. Так вот, в квантовой механике справедливо такое правило: если события различимы, складываются соответствующие им вероятности; если же события неразличимы, складываются амплитуды вероятностей. В первом случае (с подсветкой) мы имеем Р = Р1+ Р 2 = | ψ 1 |2 + | ψ 2 |2, интерференция отсутствует. Во втором случае (без подсветки) получаем: ψ = ψ 1 + ψ 2 и P = | ψ 1 + ψ 2| 2. Возникает интерференция.




