История науки знает немало примеров случайных открытий. Кто не слышал предание о том, как Архимед, принимая ванну, открыл закон о телах, погружённых в жидкость, или байку о Ньютоне, который, наблюдая за падением с дерева яблока, создал теорию тяготения? Сколько раз пытливые умы находили источник озарения в живой природе! А как много блестящих идей посетили учёных во сне! Д. И. Менделееву приснилась его периодическая таблица элементов, а Ф. Кекуле — структурная формула бензола. Но иногда важное открытие, сделанное специалистом, запоминается куда меньше, чем нехитрая закономерность, подмеченная человеком, вовсе её не искавшим, да и вообще далёким от науки. Каким-то непостижимым образом та находит его сама. И чем необычнее обстоятельства, сопутствующие этому событию, тем более яркое впечатление оно производит.
Невероятное везение профессора Смита
Один из примечательных случаев такого рода произошёл четверть века назад с любителем чисел, наблюдательным профессором психологии Гарольдом Смитом, которому (безо всякого преувеличения) крупно повезло: он сумел войти в историю математики, не имея к ней, в сущности, никакого отношения. А счастливым для Смита оказался... номер собственного телефона! Как-то профессор заметил, что этот номер, выражающийся составным семизначным числом 4 937 775, обладает любопытным свойством — сумма цифр номера равна сумме цифр всех его простых делителей:
4 937 775 = 3 · 5 · 5 · 65 837,
4 + 9 + 3 + 7 + 7 + 7 + 5 = 42,
3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42.
Быть может, этот факт так и остался бы в разряде числовых курьёзов, не вмешайся в историю родственник Смита — математик, профессор одного из американских университетов Альберт Виланский. Он опубликовал в 1982 году заметку об обнаруженном свойстве, а обладающие им составные числа назвал именем Смита. Тогда же Виланский предположил, что таких чисел существует бесконечно много. И оказался прав: вскоре эту гипотезу доказал его коллега. Так было положено начало исследованию весьма интересного множества чисел.
Самое удивительное, что изучение чисел Смита, или просто «смитов», началось с семизначного (!) числа, но ещё поразительнее то, что их не открыли гораздо раньше. Даже любой школьник знает: 2 + 2 = 4, и это никакой не курьёз!
Диковинки среди Смитов
Числа Смита обладают многими замечательными свойствами. Мы не станем на них останавливаться, заметим только, что смиты тесно связаны с другими известными математикам числами, через которые могут выражаться: репьюнитами (они записываются с помощью одних единиц) и простыми числами Мерсенна.
В семействе смитов найдётся немало настоящих диковинок! Одни числа отличаются красивым сочетанием цифр: 654, 44733, 67067. Другие — их повторяемостью: 666, 1111, 4444444444. Третьи — симметрией записи (палиндромностью): 3663, 22522, 864468. А разве не радует глаз разложение некоторых смитов на множители?
3663 = 3 · 1221 = 33 · 111,
864468 = 2 · 432234 = 111 · 7788,
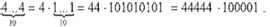
К изюминкам множества смитов можно смело отнести и десятизначные числа, у которых все цифры различные. Укажем наименьшее и наибольшее из них:
1 023 465 798 и 9 876 542 103.
А вот семизначное число 1 346 269 привлекает внимание тем, что это самый маленький смит, встречающийся в знаменитой последовательности Фибоначчи (31-й её член). Не редкость смиты и среди так называемых фигурных чисел, учение о которых восходит ещё к пифагорейцам. Так, смит 121 — квадратное число, 378 — треугольное, а 22 — пятиугольное.
Кроме того, во множестве смитов имеются примечательные пары чисел, отличающихся друг от друга всего на 1. Вероятно, по аналогии с числами-близнецами (простыми числами, отличающимися на 2), их прозвали братьями смита. Наименьшую такую пару составляют числа 728 и 729. Для примера именно она выбрана потому, что каждый из «братьев» интересен сам по себе: первый — сумма двух смитов, второй — квадрат смита:
728 = 706 + 22, 729 = 272,
то есть они оба порождены числами Смита.
Надо сказать, некоторые члены этого семейства образуются из других его представителей более простыми путями. Иногда бывает достаточно записать рядом (без пробела) два смита. Таким способом из чисел 22 и 27 получаются четырёхзначные числа Смита 2227 и 2722. В ином случае в запись исходного смита-палиндрома добавляются нули. Например, числа 22 и 535 порождают смиты 202 и 50305. Нередко нужный результат достигается простой перестановкой цифр (как в тройке смитов 319, 391, 913) или благодаря симметрии их расположения, приводящей к повтору цифр в образующихся числах (454, 45454, 454454).
В этом удивительном множестве выделяют также числа, у которых сумма цифр выражается числом Смита. Им даже дали собственное название — суперчисла Смита. Таким свойством обладают, к примеру, числа 202 (2 + 0 + 2 = 4) и 778 (7 + 7 + +8 = 22).
Особо ценятся среди смитов рекордсмены по числу цифр, присутствующих в их записи. К ним относится, в частности, исполин
9R1031 × (1069882 + 3 × 1034941 + 1)1476 × 103913210,
где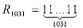 
— наибольший из известных простых репьюнитов.
В этом числе Смита насчитывается 107 060 074 цифры! С трудом верится — так компактно оно «упаковано» с помощью степеней. А знаете, сколько времени потребовалось бы, чтобы записать это число полностью? Даже при непрерывной работе с высокой скоростью письма 90 цифр в минуту на это ушло бы 2 года и 3 месяца!
«Смиты» в квадрате
В книге М. Гарднера «От мозаик Пенроуза к надёжным шифрам» приведён магический квадрат третьего порядка, составленный из чисел Смита (рис. 1). Его магическая постоянная равна 822 и является, по словам автора, наименьшей из возможных для такого квадрата.
Все указанные в клетках числа — чётные. Разделив каждое из них на 2, получим новый магический квадрат с постоянной (суммой чисел в каждой строке, каждом столбце и на диагоналях), равной 411 (рис. 2). Примечателен он тем, что состоит из девяти простых чисел; согласитесь, неплохое наблюдение автора. Но если бы дело было только в обнаруженном им свойстве… Ведь известны и другие магические квадраты, составленные из простых чисел. Однако нас сейчас интересуют вовсе не они, а числа Смита. Какое отношение имеют они к получившейся таблице?
Приглядитесь внимательнее, и вы заметите, что суммы некоторых её чисел дают числа Смита. Так, в простейшем случае
11 + 47 = 58.
Разность магической постоянной 411 и числа 137 из центральной клетки равна другому представителю семейства смитов — числу 274. Это означает, что сумма любых двух простых чисел, занимающих центрально-симметричные клетки квадрата, оказывается числом Смита:
11 + 263 = 83 + 191 = 47 + 227 = 101+ + 173 = 274.
А вот ещё один любопытный факт: суммы пар чисел, стоящих вдоль линий, параллельных главным диагоналям, также равны числам Смита. Действительно:
11 + 83 = 94, 83 + 263 = 346,
263 + 191 = 454, 191 + 11 = 202.
Все пять смитов есть в исходной таблице и, что характерно, красиво располагаются в её угловых клетках и в центре (рис. 1), в то время как сами слагаемые размещаются в средних клетках по сторонам второй таблицы (рис. 2). Если собрать все девять чисел в новую таблицу (рис. 3), они образуют двойной симметричный узор (рис. 4).
К тому же теперь наглядно видно, как просто и разумно связаны между собой тройки чисел, входящих в каждое из четырёх последних равенств (рис. 5, 6).
Можно также рассматривать суммы трёх или более чисел второго квадрата, при выборе которых логично руководствоваться симметрией их расположения — к примеру, относительно главной диагонали. Возьмём для определённости диагональ квадрата, идущую из левого нижнего в правый верхний угол. Она даёт три числа: 101, 137 и 173. Добавим к ним ещё четыре: 47, 263, 227 и 83 (рис. 7).
Оказывается, их различные комбинации приводят к разным числам Смита. Скажем, каждая из троек 47, 263, 173 и 227, 83, 173 при сложении даёт 483.
47 + 263 + 173 = 227 + 83 + 173 = 483.
Весьма любопытная картина вырисовывается при игре с четвёрками чисел. Легко заметить, что смит 483 получается также при сложении 346 и 137 (оба числа встретились в рассмотренных магических квадратах, рис. 1 и 2). Тогда смит 346 можно представить в виде разности 483 и 137:
(47 + 263 + 173) – 137 = (227 + 83 + +173) – 137 = 346.
Аналогично 483 = 382 + 101, откуда 382= 483 – 101, или (47 + 263 + 173) – 101 = (227 + 83 + 173) – 101 = 382.
Пойдём дальше: 274 = 411 – 137, где 411 есть магическая постоянная второго квадрата, а значит, выполняются равенства
(47 + 263 + 101) – 137 = (227 + 83 + 101) – 137 = 274.
Итак, задействовав возможные пары чисел главной диагонали этого квадрата, удалось «сконструировать» три числа Смита, присутствующие в исходном квадрате: 346, 382 и 274. И если в первый раз такой результат мог быть случайностью, а во второй — простым совпадением, то в третий раз начинает проявляться вполне определённая закономерность. А какой истинный любитель математики откажется её проверить?
Если теперь ограничиться рассмотрением чисел 47, 263, 83 и 227, нетрудно получить хотя и не столь очевидные, но уже вполне ожидаемые и даже предсказуемые результаты:
227 + 83 – 263 + 47 = 94,
227 + 83 – 47+263 = 526,
47 + 263 – 227 + 83 = 166,
47 + 263 – 83 + 227 = 454.
И вот перед нами ещё четыре смита из исходного квадрата. Любопытно, что они занимают такие же клетки, что и числа второго квадрата, из которых получены. Мозаика почти сложилась, осталось всего ничего — выразить ещё два смита: 22 и 202. А в том, что эта задача разрешима, сомнений не осталось.
Воспользуемся тем, что уже известно. Ближайший к числу 22 смит из составленного Гарднером магического квадрата — число 94; 22 = 94 – 72, или (227 + 83 – 263 + 47) – (173 – 101) = 22.
Аналогично 202 = 166 + 36, или (47 + 263 – 227 + 83) + (173 – 137) = 202. Впрочем, в этом случае можно обойтись и четвёркой чисел: 202 = 303 – 101 = 47 + 83 + 173 – 101.
Между тем попытки выразить аналогичным образом число 22 приводят к ещё одному открытию: оказывается, смиты из исходной таблицы можно получить из четвёрок чисел, занимающих соседние центрально-симметричные клетки второй таблицы (рис. 8), например:
58 – 36 = (47 + 11) – (263 – 227) = 22,
58 + 36 = (47 + 11) + (263 – 227) = 94,
(173 + 83) – (191 – 101) = 166,
(173 + 83) + (191 – 101) = 346.
Получается изящная головоломка: как, имея набор простых чисел, составить простейший магический квадрат из составных чисел Смита, да ещё и с наименьшей постоянной?
Такие простые закономерности…
Поразмышляв немного, вы обнаружите и, возможно, обоснуете немало интересных закономерностей, связывающих числа Смита. А начать можно с чего-нибудь совсем простого.
Скажем, 58 – 36 = 22, а 58 + 36 = 94, откуда 58 = (22 + 94) : 2, следовательно, смит 58 — среднее арифметическое смитов 22 и 94. В свою очередь 94 — среднее арифметическое 22 и 166, а вот число 22 — среднее геометрическое смитов 4 и 121 (22 =2 · 11 =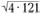 
).
Или другой пример. Выпишем по порядку первые пятнадцать чисел Смита и выделим из них каждое второе:
4, 22, 27, 58, 85, 94, 121, 166,
202, 265, 274, 319, 346, 355, 378.
Посмотрите, как интересно они связаны:
22 = 58 – 62 = 94 – 2 · 62 = 166 – 4 · 62,
22 = 265 – 1 · 35 = 319 – 11 · 33 = 355 – 111 · 3.
А вот ещё одно наблюдение. Оно касается многозначных чисел Смита, у которых всего два простых множителя.
22 = 2 · 11 = 22 + 0, 2 + 1 + 1 = 2 + 2 + 0 = 4,
58 = 2 · 29 = 22 + 36, 2 + 2 + 9 = 2 + 2 + 3 + 6 = 13,
85 = 5 · 17 = 22 + 63, 5 + 1 + 7 = 2 + 2 + 6 + 3 = 13,
94 = 2 · 47 = 22 + 72, 2 + 4 + 7 = 2 + 2 + 7 + 2 = 13.
Как видим, если такое число представить в виде суммы двух слагаемых, причём одно из них 22 (смит), то сумма цифр его множителей будет такой же, как и сумма цифр слагаемых, и равна либо 4, либо 13.
Оказывается, аналогичным свойством обладают и трёхзначные числа Смита, при этом повторяется слагаемое 202 (снова смит!), а суммы цифр равны 4, 13 или 22. Например:
355 = 5 · 71 = 202 + 153 (суммы цифр — 13),
778 = 2 · 389 = 202 + 576 (суммы цифр — 22).
Любопытно также, что у всех ключевых чисел (4, 13, 22, 202) сумма цифр равна наименьшему смиту, а два из них (22 и 202) — суперчисла Смита.
Можно изучать самые разные группы смитов и даже отдельных представителей этого семейства, открывая всё новые и новые их свойства. Чем, например, примечательна тройка 27, 58 и 85? Что общего у чисел 4, 121 и 10 201? А какое отношение к смитам имеет число 31? Как говорил в таких случаях один из героев Гарднера, не существует ни одного числа, которое не обладало бы какими-нибудь необычными свойствами. И представители многочисленного семейства смитов лишь подтверждают это.
Словарик к статье
Репьюниты (от англ. repeated unit — повторенная единица) — натуральные числа, в записи которых присутствуют только единицы: то есть R1 = 1, R2 = 11, R3 = 111 и т. д., в общем виде Rn = (10n – 1) : 9, где n = 1, 2, 3… — числа натурального ряда.
Простые числа Мерсенна — простые числа вида Mp = 2p – 1, где p также простое число 2, 3, 5, 7, 13, 17, 19, 31… (М11 простым не является). Вероятно, самое большое известное простое число Мерсенна — М216091 имеет 65 050 цифр.
Ряд Фибоначчи — числовой ряд 1, 1, 2, 3, 5, 8, 13, 21… каждый последующий член которого равен сумме двух преды- дущих: An = An–1 + An–2. Ряд интересен тем, что отношение двух соседних членов ряда в пределе даёт «золотое сечение» — отношение частей поделённого отрезка 0,62 : 0,38. Например, уже 13 : 21= = 0,619 ≈ 0,62.
