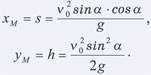С Луны на Землю
Каким бы фантастическим ни казался рассказ Мюнхаузена, в нём есть разумное зерно — сам подход к решению проблемы. Барон, конечно, знал, что кратчайший путь пролегает вдоль прямой. Поэтому решил «построить» из кусков верёвки прямую, вернее, её часть — отрезок, один конец которого должен был находиться на Луне, а другой — на Земле (отрезок AB на рис. 1, его длина определяет расстояние между телами).
С точки зрения геометрии такое построение возможно. Оно основано на известных утверждениях: через любые две точки можно провести прямую, и притом только одну; из трёх точек прямой только одна лежит между двумя другими. Прямая бесконечна, а отрезок нет, так что, начав движение из точки A и сделав конечное число «шагов», барон окажется в точке B — вернётся с Луны на Землю.
Не может быть!
Согласно законам геометрии, двуногий конь не сумеет принять на земле устойчивое положение и упадёт, а значит, не сможет мирно пастись на лугу, тем более брыкаться и разгонять турок ударами копыт! Устойчивое положение объекта достигается при опоре на три точки при условии, что они не лежат на одной прямой. Это следует из известной аксиомы стереометрии: через любые три точки, не лежащие на одной прямой, проходит плоскость, причём только одна (см. «Наука и жизнь» № 11, 2009 г.).
Внутрь рыбы!
Съёжившись в комок, Мюнхаузен придал своему телу шарообразную форму. «Остроумная хитрость» состояла в том, что барон выбрал оптимальную форму, приняв которую можно было легко и без вреда для здоровья проскользнуть внутрь рыбы. Во-первых, из всех тел именно шар имеет минимальную площадь поверхности и, значит, потенциально меньше точек соприкосновения с зубами рыбы. Во-вторых, в воде шарообразная форма хорошо обтекаема, динамична и может легко видоизменяться. Не случайно, отмечают биологи, форма шара свойственна многим живым организмам, населяющим однородную среду (икринки рыб, морские ежи, некоторые виды бактерий, водорослей и планктона).
Точка столкновения
Как известно, выпущенный из пушки под углом α к горизонту снаряд движется по кривой. Если пренебречь сопротивлением воздуха, можно считать его траекторию параболической. При одинаковых условиях полёта (исходной высоте над уровнем земли, начальной скорости v0 и угле α) два одинаковых ядра, выпущенные одновременно из нацеленных друг на друга одинаковых пушек, опишут в воздухе ветви одной и той же параболы и столкнутся в её вершине — точке M (рис. 2).
Итак, задача сводится к вычислению координат точки M, а для этого вполне хватит школьных знаний. В курсе кинематики доказывается, что уравнение такой параболы имеет вид:
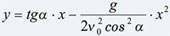
где g — ускорение свободного падения. А из курса алгебры известно: вершина М параболы y = ax2 + bx + с имеет
координаты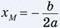 
yМ = y(xМ).
Немного терпения и тригонометрических преобразований, и ответ готов:
