Плоские кривые, в частности конические сечения — эллипс, парабола и гипербола, с античных времён используются для решения целого ряда задач, в том числе предложенных в предыдущем номере. Ответы на них помогут проверить правильность ваших решений.
Древняя рогулька
Инструмент для построения двух и более окружностей разного радиуса, очевидно, должен представлять собой циркуль с несколькими ножками, число, местоположение и длину которых можно при необходимости изменить. Две простейшие конструкции показаны на рис. 1.
Построить окружности разного радиуса циркулем с фиксированным раствором можно так. Сначала следует начертить окружность на бумаге, как обычно, затем приподнять конец циркуля и опереть его, скажем, на кубик, а другим концом описать ещё одну окружность — она будет меньшего размера (рис. 2). Второй способ — начертить окружность на поверхности фигуры, в сечении которой она может получиться: например на шаре, конусе (рис. 3) или ином подходящем теле вращения.
С помощью таких нехитрых приёмов и приспособлений легко нанести рисунок из концентрических или пересекающихся окружностей и дуг, например, на глиняную посуду. Подобные узоры (их называют циркульными) встречаются на многих древних сосудах, на их поверхности видны даже отметки от острия циркуля (фото 4).
Догадка Тартальи
При отсутствии сопротивления воздуха ядро, выпущенное из пушки со скоростью ν0 под углом a к горизонту, движется по параболе, ветви которой направлены вниз:
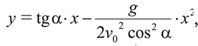 ,
,
где g — ускорение свободного падения.
Ордината точки падения ядра y0 = 0, тогда абсцисса этой точки, то есть искомое расстояние 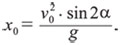
Эта величина достигает наибольшего значения при sin 2α = 1, или 2α = 90°, α = 45° (рис. 5). Значит, результат, полученный Никколо Тартальей экспериментально, правильный.
Добавим, что sin 2α = sin (180° — 2α) = sin 2(90° — α).
Это означает, что два ядра, выпущенные из пушки под углами, дополняющими друг друга до 90°, например 30° и 60°, попадут в одну точку. И ещё один интересный факт. Если рассмотреть все траектории, которые получаются при начальной скорости ядра ν0 и углах 45° ≤ α < 90°, то они будут касаться одной линии — и это тоже парабола! Её называют параболой безопасности (рис. 6). Ни в какой объект, находящийся за пределами ограниченной ею области, снаряд не попадёт.
Инструмент да Винчи
Если угол между осью конуса и образующей равен углу между секущей плоскостью и осью конуса, то в сечении получится парабола. Так будет, в частности, при пересечении прямоугольного конуса плоскостью, перпендикулярной образующей (рис. 7). Это свойство подсказывает, как изготовить параболический циркуль. Конструкция должна иметь две ножки: неподвижную, опорную (представляет ось конуса), и вращающуюся, составляющую с ней угол 45° (играет роль образующей, а точнее, её отрезка от вершины конуса до линии сечения). Первая ножка — фиксированной длины, вторая — переменной; по сути, это трубочка, в которой свободно скользит стержень, рисуя параболу. Такова и конструкция Леонардо да Винчи, которую он укрепил на треноге.
Во Флоренции, в Музее истории науки, представлена действующая модель циркуля, изготовленная в 2001году по эскизу Леонардо да Винчи (рис. 8). Парабола чертится на листе бумаги на наклонной плоскости, параллельной одной из «ног» треноги, причём в два шага: сначала одна ветвь, затем другая, начиная с вершины. Стержень соскальзывает вниз под тяжестью собственного веса и веса прикреплённого на нитке груза.
Добавим, что конструкция совершенного циркуля аналогична той, что придумал Леонардо да Винчи, но более мобильна: она позволяет варьировать углы между осью конуса и образующей и между секущей плоскостью и осью конуса. Иными словами, всегда можно наклонить опорную ножку к плоскости листа под определённым углом и выбрать раствор циркуля так, чтобы начертить то или иное коническое сечение. Однако на практике удобнее пользоваться стационарной моделью и изменять положение секущей плоскости.




