ИЗМЕРЕНИЕ РАДИУСА ЗЕМЛИ
История свидетельствует, что первые высказывания о шарообразности Земли принадлежат древнегреческому ученому Пифагору (примерно 571 - 497 годы до и. э.).
Размеры земного шара впервые (когда сохранился и метод, каким они получены) были установлены александрийским ученым Эратосфеном в III веке до нашего летосчисления. Для своих расчетов Эратосфен использовал разницу в положении Солнца в день летнего солнцестояния (22 июня) в двух городах - Александрии и Сиены (ныне Асуан), находящихся, по его предположению, на одном меридиане. В полдень 22 июня в Сиене Солнце отражается в глубоких колодцах, то есть, как говорят, стоит в зените - при этом предметы не дают тени. В тот же день, и в то же самое время в Александрии вертикально стоящие предметы отбрасывают тень. По величине ее Эратосфен определил, что в Александрии Солнце не доходит до зенита на 7° 12', что соответствует /so окружности Земли на таком расстоянии друг от друга лежат города Сиена и Александрия.
Длину пути между этими городами Эратосфен вычислил, отсчитывая шаги верблюдов, на которых в то время купцы перевозили своп товары. Оставалось умножить полученную цифру на 50, чтобы узнать длину всей земной окружности по меридиану. По его подсчетам, она оказалась равной (в современных мерах) 39 500 километрам. Отсюда он получил радиус Земли - 6 310,5 километра.
К концу IX века размеры радиуса Земли были определены неоднократно, но разные результаты «явились пунктом преткновения, побуждающим к возобновлению проверки и измерения», как писал Беруни. Он задался целью установить более точные размеры Земли. Способ, каким пользовался Эратосфен, требовал значительных материальных средств и участия большого числа людей для линейных измерений. Беруни, судя по его замечанию, не располагал ни тем, ни другим «Но кто будет со мной участвовать в этом? Ведь он нуждается в силе, поскольку ему необходимо покрывать большие пространства в измеряемой местности, как нуждается он, и в охране от зол, причиняемых рассеянными по ней недругами»
Как выход из создавшегося затруднения Беруни применил способ «понижения горизонта», то есть «другой путь для определения окружности Земли без необходимости хождения по пустыне, а именно поднимемся на высокую гору, стоящую на берегу моря или возвышающуюся над ровной низиной. Когда мы найдем такое место у моря или в пустыне, будем наблюдать Солнце с горы на восходе или закате, пока не скроется из нашего зрения половина его диска. Тогда мы замерим его понижение с помощью армилярной сферы с алидадой»
Сущность этого способа заключается в следующем. Допустим, что высота горы AD = h известна, и с ее вершины Л измерен угол «понижения горизонта» ц (см. рис.).
Прямые АВ, и АМ - касательные к поверхности Земли, где радиус R = OD. В этом случае малый круг СМВ будет представлять видимый горизонт. Из рисунка следует, что
![]() ,
,
Откуда
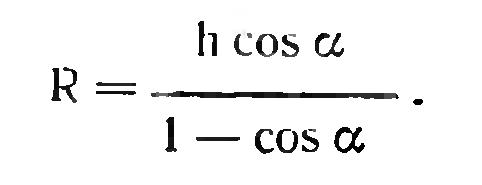
По этой формуле Беруни вычислил радиус Земли и получил R = 6 339,58 километра, что достаточно близко подходит к величине радиуса Земли, каким мы пользуемся теперь (R = 6 371,11 километра).
Беруни понимал, что это непростая задача и, что полученные им результаты могут отличаться от расчетов других авторов. Он писал; «Неизбежно, что относительно измерения Земли должны существовать противоречия, так, как научные вопросы подобного рода должны основываться на длительном опыте и наблюдательных данных. Все народы сообщали (см. табл. - Л. X.) свои наблюдения по этому вопросу в своих единицах, которые применяются в их стране. Так, например, греки - в стадиях, индусы - в Йоханах. Когда их книги были переведены на арабский язык, то действительная величина их единиц измерений была неизвестна»
Свои измерения для определения радиуса Земли Беруни произвел в Индии с вершины горы, находящейся около крепости Нандна. При этом угол понижения горизонта он измерял астролябией, а высоту горы для контроля дважды определил при помощи сконструированного им самим высотомера и получил одинаковые результаты.
УСОВЕРШЕНСТВОВАНИЕ АСТРОЛЯБИИ
Примитивные астрономо-геодезические инструменты были известны еще со времен глубокой древности. Некоторые из них, такие, например, как астролябия, использовались для определения географических координат вплоть до XVIII века. Беруни неоднократно пользовался астролябией при астрономических и геодезических работах для определения углов, как в горизонтальной, так в вертикальной плоскостях и внес значительные усовершенствования в этот прибор.
До Беруни астролябия представляла собой два плоских круга с диоптрами, один из которых перемещался внутри другого, с угловыми делениями, нанесенными по его внутреннему диаметру. Такими приборами астрономы могли лишь определять эклиптикальные координаты звезд.
Беруни создал оригинальную конструкцию шаровой астролябии, при этом раздвинулись возможности использования прибора. Новая астролябия позволила следить за восходом и заходом звезд, за их движением на разных широтах и решать большее число задач, чем это было доступно для плоских астролябий. В подробных трактатах Беруни рассказал не только о конструкции своих приборов, но, и о возможностях и правилах работы с ними, о новых, раскрывающихся способах исследований.
ОПРЕДЕЛЕНИЕ «НЕПРИСТУПНОГО РАССТОЯНИЯ»
Способ, каким Беруни предложил определять ширину реки, оврага, глубину колодца или другое «неприступное расстояние», не потерял своего практического значения и до сих пор.
Чтобы определить, например, ширину реки, оврага - ВС, он предлагает построить два равных прямоугольных треугольника ЛСВ, и ACD с общей стороной АС. Наблюдатель, находясь на одном берегу реки, например, в точке А, при помощи астролябии измеряет угол ВАС, и такой же угол строит при точке А, и сторону его АМ закрепляет, поставив на местности веху, например, в точке М. После этого, продолжив на местности направление прямой ВС в сторону вехи М, отыскивают на ней точку D, которая лежала бы на пересечении прямых ВС, и АМ. Теперь остается измерить расстояние DC, которое равно ширине реки ВС.
Аналогичным способом Беруни измеряет глубину колодца AC = h. От края колодца, например, из точки А продолжить прямую СА на некоторое расстояние АВ = а, и измерить при помощи астролябии два угла, а, и р соответственно при точках Л, и В, визируя алидадой астролябии каждый раз на точку D, находящуюся на дне колодца DC. Из треугольников ACD, и BCD следует, что
![]()
Так, как,
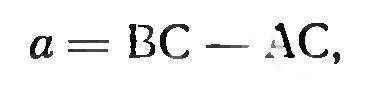
то с учетом предыдущего следует, что,
![]()
откуда
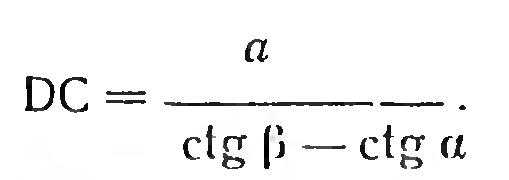
искомая глубина колодца
![]()
или
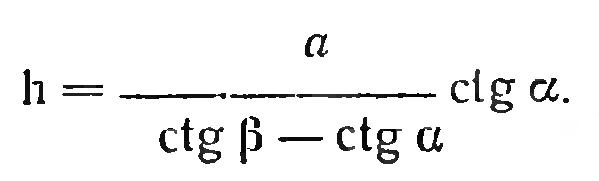
Полученные результаты я закреплял в записях и не запоминал их наизусть, надеясь на спокойствие и безопасность от бедствий. Когда же беда застигла меня врасплох (вынужденный отъезд из города Кята. - Л. X.), она погубила все упомянутое так же, как и плоды всех других моих стараний.
Глобус позволил Беруни правильно решать вопрос о кратчайшем расстоянии между пунктами на земной поверхности, которые он рекомендовал определять по дуге большого круга.
Глобус, сделанный Беруни, к сожалению, не сохранился.
ПРИБОРЫ ДЛЯ ОПРЕДЕЛЕНИЯ ГЕОГРАФИЧЕСКОЙ ШИРОТЫ
Беруни - автор нескольких приборов специально предназначенных для определения географических широт трехшестового, конусного, шестового и гномонного. Описание этих приборов и правила пользования ими он приводит в своей «Геодезии»
Так, например, про свой трехшестовын прибор он пишет «Сделаем из любого материала три ровных и равных шеста EK, EL, и ЕМ. Затем замерим положение звезды в три любых момента времени в течение одной ночи, но чем больше будет промежуток между ними, тем надежнее результат. Пусть будут положения звезды на параллели в эти три момента времени G, Н, и F.
Соединим основание шестов в точке Е стержневыми замками и будем наблюдать посредством каждого из шестов эту звезду
ГЛОБУС БЕРУНИ
Глобус - уменьшенная модель, наиболее достоверно отражающая форму нашей планеты, - впервые был изготовлен примерно в 150 году до и. э. Кратесом Миллосским, придворным ученым царя Аттаза. А первое подробное описание способов изготовления глобусов с географической сеткой было приведено К. Птолемеем (87 - 165 голы), в его известном «Руководстве по географии»
Есть все основания считать, что первым из ученых попе Птолемея глобус сделал Беруни. Это было в самом конце IX или в начале X века.
Живя в городе Кяте, Беруни, как пишет П,- Булгаков, построил «один из первых научных глобусов в Средней Азии и на Ближнем Востоке, на котором были отмечены населенные пункты с точностью, позволяющей определять их географические координаты.» Далее II. Булгаков пишет, что, создавая своп глобус, Беруни преследовал подлинно научные цели. «В какой-то мере он, видимо, руководствовался указаниями Птолемея, труды которого были ему хорошо известны, но решил эту задачу на базе собственного материала и данных средневековых среднеазиатских географов, в частности Джейкани»
А о том, как Беруни создавал свои г то-бус, он рассказывает сам «Я упорно трудился в прошлом над соединением метода Птолемея, изложенного в книге «География», с методами ал-Джейхана и других ученых, которым они следуют в «Книгах о путях»; я собрал рассеянное, разъясняя неясное и пополняя эту отрасль знаний. Я начал с уточнения расстояний и названий мест и городов, основываясь на слышанном от тех, кто по ним странствовал и собранном из уст тех, кто их видел. Предварительно я проверил надежность материала и предпринял меры предосторожности путем сопоставления сведений одних лиц со сведениями других.
Я не жалел ни сил, ни денег, желанных для меня, на пути к достижению этой цели и изготовил для мест и городов полушарие диаметром в десять локтей (около 5 метров. - Л. А.), чтобы определять по нему долготы и широты их расстояний, так, как время не позволяло применять математические расчеты для их вычисления из-за множества расстояний и длительности расчетов. в одно из трех времен либо скольжением взгляда вдоль шеста, к которому должен припасть взором наблюдатель либо, как обычно, с помощью двух находящихся на нем просверленных диоптров.
Когда мы это сделаем и ЕК окажется на прямой KG, EL - на LH, а ЕМ - на прямой MF, все эти шесты окажутся на поверхности, образующей конус, вершина которого - центр вселенной, а основание - окружность суточной параллели светила.
Вследствие равенства шестов их концы, то есть К, L, и М, будут на линии окружности, параллельной суточной параллели ABD.
Соединим К, и М тонкой, крепкой нитью и прикрепим к концу шеста L линейку, по которой будет скользить конец шеста и не будет мешать двигаться линейке, пока она не столкнется с плоскостью горизонта. Затем будем двигать линейку поверх нити КМ, не нажимая на нее, пока она не достигнет плоскости горизонта в точке S. находящейся в плоскости окружности основания конуса.
Безусловно, S будет на линии пересечения плоскости (основания конуса) с плоскостью горизонта, а эта линия параллельна AD. Вследствие этого проведем (линию) SP перпендикулярно к ВС. Опустим из L перпендикуляр на плоскость горизонта. Проведем из (точки) О, являющейся местом падения камня из L. к Р линию, параллельную ВС. Соединим L с Р, и тогда угол LPO будет равен дополнению широты города, так, как линия LP, находящаяся в плоскости окружности конуса, параллельна линии, соединяющей С с серединой дуги AD.
Треугольник PLO подобен треугольнику, образованному перпендикуляром, опущенным из середины дуги AD на плоскость горизонта и двумя линиями, соединяющими С с обоими концами этого перпендикуляра, а эти две линии и образуют угол дополнения широты города. Следовательно, угол LPO равен величине дополнения широты города»
Пользуясь своими приборами, Беруни довольно точно определял географические координаты разных мест и городов. Например, по его вычислениям, широта Бухары - 39°20' (по современным данным - 39'48'). Ургенча - 42°17' (41°35'), Чарджоу - 39°12' (39°08').




