Теорема о биссектрисе треугольника — двумя сгибами бумаги
Известная теорема о биссектрисе внутреннего угла треугольника гласит, что такая биссектриса делит противоположную сторону в отношении, равном отношению двух прилежащих сторон, то есть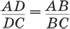 
(рис. 1).
Существует несколько методов доказательства этой теоремы. В них проводится значительное число геометрических построений, рассчитываются площади треугольников либо используется теорема синусов и другое.
Покажем, как просто доказать эту теорему, используя лист бумаги. (Применение этого метода для другого случая продемонстрировано в статье: «Математика без математики на листе бумаги» — см. «Наука и жизнь» № 2, 2025 г., стр. 90.)
Вырежьте из бумаги два одинаковых треугольника (рис. 2). Почему два — станет ясно чуть далее.
Согните один из треугольников, совместив сторону АВ со стороной ВС. В результате край бумаги BD будет являться биссектрисой угла B исходного треугольника (рис. 3), по-скольку равны углы ABD и А' BD — они совпали при наложении...
