Длина ребра правильных пирамид, из которых сложен додекаэдр, при условии, что все вершины пирамид сходятся в одной точке, будет равна радиусу R шара, описанного вокруг додекаэдра, а также половине большой диагонали куба, вписанного в додекаэдр.
Сторона этого куба равна стороне звездчатого правильного пятиугольника ACEBDA с теми же вершинами, что и правильный выпуклый пятиугольник АВСDЕ - основание правильной пирамиды.
На рисунке - ортогональная проекция правильного додекаэдра на плоскость. Проекция грани АВСDЕ и сама грань равны оригиналу. В натуре ребра АВ=М1М2=АМ 1=М2М3... Проекция вершин М1, М2, ... М10 - правильный десятиугольник. Соединив четыре вершины додекаэдра, можно получить (в натуре) квадрат. Какие это вершины и сколько взаимно ортогональных квадратов может быть получено?
Предположим, что наш додекаэдр сделан из сыра. Срезав с него шесть одинаковых частей (обелисков), в основании которых будет квадрат со стороной, равной длине стороны названного звездчатого пятиугольника, получим тот самый куб, вписанный в додекаэдр.
Построение правильного пятиугольника (по Дюреру)
Дано АВ = а. Проводим окружности с центром в точках А и В радиусом а. Отметим точки С и D. АВ = АD = ВD = а. Проведем окружность радиусом DA из центра D. Проведем прямую СD, отметим точку Е. Проведем прямые FEH и GEK. Отметим точки К и Н. Из них, как из центра, сделаем засечки радиусом а, получим точку L и правильный пятиуголь ник АВНLK. Построение приближенное, но достаточно точное.
Построение правильного пятиугольника, вписанного в окружность радиуса r (по Птолемею)
Дана окружность радиусом r = ОА.
Отметим точку Е (ОЕ = ЕА) и точку D (OD ^ ОА). Из точки Е, как из центра, проведем дугу радиусом ЕD до пересечения с прямой АО. Отметим точку F. Отрезок ЕF = ED. Сторона правильного пятиугольника а5, вписанного в окружность радиуса r, равна длине отрезка DF.
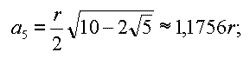
r = 0,8506 а5.
Отрезок DM - сторона правильного звездчатого пятиугольника
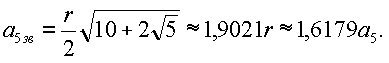
Зная, что ребро куба равно а5зв, легко определить его диагональ и радиус описанного шара, равный длине ребра пирамидки. R " 1,4а5.
Если а = 35 мм, то длина ребра пирамидки равна " 49,5 мм.




