ОТВЕТЫ И РЕШЕНИЯ. ИЮНЬ 1999 №6

1. Каждое число в данной последовательности есть сумма квадратов цифр предыдущего числа, поэтому вместо многоточия надо поставить число 20(20=4²+2²).

Комментарий. Эта задача, формально доступная ученику начальной школы, на самом деле достаточно нетривиальна. Тем не менее были абитуриенты (примерно каждый пятидесятый), решившие эту задачу. Разумеется, можно предлагать и более простые (но и более сложные!) закономерности.

2. Сначала надо заполнить больший сосуд, после чего отлить из него в меньший 4 литра. Затем вылить из меньшего сосуда воду и перелить в него оставшиеся 3 литра из большего сосуда. Снова залить из крана больший сосуд и вылить из него 1 литр в меньший (ведь там оставалось 3 литра). Тогда в большем сосуде будет как раз 6 литров воды.

Комментарий. Хотя задачи на переливание считаются классическими среди головоломок, однако, даже зная некоторые примеры такого рода, к ним трудно подготовиться.

3. Сначала три раза откладываем от точки А в выбранном направлении меньший отрезок (точнее, меньшую линейку), получая в итоге отрезок АВ длиной 3^.9=27 см. Затем от точки В в обратном направлении откладываем два раза больший отрезок, получая отрезок ВС длиной 2^.13=26 см. Тогда отрезок АС длиной 27-26=1 см и будет искомым. Разумеется, точно такой же отрезок можно отложить от точки А и в противоположном направлении. То есть задача допускает два решения.

Комментарий. К сожалению, задачи на построение (даже такие простые, как эта), украшающие элементарную геометрию, практически не встречаются в практике вступительных экзаменов.

4. Нетрудно заметить, что |х|=xЧ sign x. Поэтому при 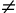х 2, х 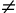3 исходное уравнение равносильно следующему:

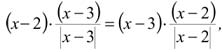
откуда |х-3|=|х-2|, т. е. х=2,5. Осталось отдельно рассмотреть случаи х=2 и х=3; отсюда находим еще два корня х=2 и х=3. Таким образом, уравнение имеет три корня: х₁=2; х₂=3; х₃=2,5.

Комментарий. Любопытно, что эту в общем-то безобидную и достаточно несложную задачу решили лишь 2% абитуриентов, хотя многие из них решали с репетиторами стандартные задачи на уравнения с модулями. А эту задачу в принципе можно решить так же, рассматривая разбиение числовой оси на интервалы знакопостоянства. Но непривычная ситуация, совершенно неизвестная доселе функция наводили на большинство поступающих панический ужас, некоторые бросали задачу, даже не дочитав ее до конца, а потом жаловались, что в билетах даются какие-то непонятные функции.

5. Из второго уравнения системы имеем

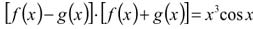
откуда с учетом первого уравнения

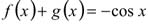
при х 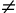0. Сложив полученное уравнение с первым уравнением системы, получим

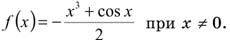
Аналогично: .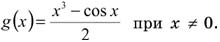

Наконец, при х=0 из исходной системы получим лишь, что f(0)=g(0), т. е. окончательно:

.

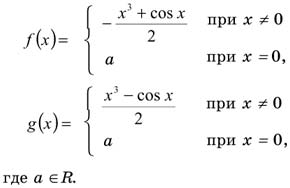6. Да. Более того, этот треугольник будет подобен исходному, что легко следует из теоремы синусов. В самом деле, если а, b и с - соответствующие стороны данного треугольника, то по этой теореме

.

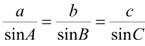Комментарий. Заметим, что, применив теорему косинусов к треугольнику со сторонами sin A, sin B и sin C (напомню, что этот треугольник подобен исходному, а угол С лежит напротив стороны sin C), получим изящное геометрическое доказательство достаточно нетривиального тригонометрического тождества (для любых углов А, В и С, таких, что А+В+С=):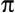

.

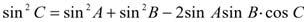7. Действительно, пусть е₁ и е₂ две "единицы". Покажем тогда, что они равны. Так как е₁ - "единица", то по определению е₁*е₂ =е₂. С другой стороны, е₂ - тоже "единица", поэтому е₁*е₂ =е₁. Отсюда е₁=е₂ , что и требовалось.

Комментарий. Для человека, прочитавшего хотя бы пару страниц из любого учебника по теории групп, эта задача покажется элементарной, но ведь в школе этого не проходят. А потому такая задача может дать неплохое представление об уровне абстрактного мышления абитуриента.

ПРИМЕР НА СЛОЖЕНИЕ (№ 5, 1999 г.)

Поскольку все цифры в первой слева колонке значимые и три из них различны, И не может быть меньше 8 (И - четное число), но и больше 8 быть не может. Следовательно, И = 8, а Г = 2. Продолжая анализ, придем постепенно к решению:

СОН В РУКУ (№ 6, 1999 г.)

— Да, — выслушав эту смачную историю, снова повторил инспектор, — старина Лайерс и впрямь был очень колоритной фигурой, вот только один недостаток...

— Да что вы заладили про этот недостаток? — не выдержал Глум. — Что вы имеете в виду?

— Ничего особенного. — Борг вовсю улыбался. — Просто сержант Лайерс очень любил приврать.

— С чего вы взяли? — не унимался Глум.

— Подумайте сами. Если Чанк действительно умер во сне, то откуда же было известно, что ему снилось.

— А ведь верно. — Глум восхищенно щелкнул пальцами. — Как я сам не догадался! Ну и дока же вы инспектор! Хотя, постойте, постойте... — сержант подозрительно посмотрел на напарника. — А как же тогда быть с вашей историей?! Откуда вы могли узнать про тень и так далее? И, кстати, от кого вы все это услышали?

— Сержант Глум, — строго кашлянув, инспектор попытался скрыть смущение, — вы совсем забыли про нашу работу!

И, прикрывшись газетой, инспектор Борг стал пристально вглядываться в старинное здание на другой стороне улицы.

КАК МУЖИК С ЧЕРТОМ СПОРИЛ, ИЛИ ТРЕУГОЛЬНИКИ ИЗ СПИЧЕК (№ 4, 1999 г.)

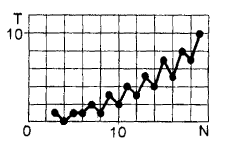
На графике видно, что если к любому нечетному числу спичек добавить три спички, то число возможных треугольников не изменится, а если добавить одну - то даже уменьшится (кроме случая N=5).

По три треугольника можно построить из 9 и 12 спичек (со сторонами 3-2-4, 3-3-3, 4-4-1 и 4-4-4, 5-4-3, 5-5-2 соответственно). У мужика оставалось именно 12 спичек, так как он обещал отдать ровно половину. Две спички были потрачены на костер, значит, в лес он въехал с 14 спичками.

ОТВЕТЫ НА КРОССВОРД С ФРАГМЕНТАМИ (№ 5, 1999 г.)

По горизонтали. 5. Ильюшин (советский авиаконструктор; на снимке — штурмовик Ил-2). 6. «Москвич» (автомобиль, изображенный на снимке, со специальным кузовом). 8. Самарканд (город в Узбекистане; на снимке — медресе Улугбека). 11. Ермак (представлен фрагмент картины «Покорение Сибири Ермаком» В. Сурикова). 14. Палец (деталь двигателя внутреннего сгорания, разрез которого представлен). 15. Ордовик (один из перечисленных периодов палеозойской эры). 16. Пальма (на снимке — финиковая пальма). 17. Осипов (президент Российской академии наук с 1991 г.). 20. Антенна (деталь поплавка). 22. Червь (перевод с английского). 23. «Анчар» (стихотворение А. Пушкина, строки из которого приведены). 26. Семинария (православное духовное учебное заведение). 27. Калория (внесистемная единица количества теплоты, определение которой приведено). 28. Гарднер (американский популяризатор науки, приведена задача из его сборника «Есть идея!»).

По вертикали. 1. Алгебра (приведено несколько алгебраических формул). 2. Лиман (залив или озеро, образующееся при затоплении морем долины равнинной реки). 3. «Волны» (цикл стихотворений Б. Пастернака, строки из которого приведены). 4. Тимашев (министр внутренних дел Российской империи в 1868—1878 гг.; приведены строки из стихотворения «История государства Российского от Гостомысла до Тимаева» А. Толстого). 7. Протон (ядро атома водорода). 9. Максакова (советская оперная певица; на снимке — в роли Марфы из оперы «Хованщина» М. Мусоргского). 10. Карборунд (абразивный материал, химический состав которого приведен). 12. Грумант (старинное русское название островов Шпицберген, карта которых приведена). 13. Миксина (животное класса круглоротых). 18. «Менины» (представленный автопортрет испанского художника Д. Веласкеса является фрагментом этой его картины). 19 Сенегал (государство в Африке, герб которого представлен). 21. Галилей (итальянский ученый, первооткрыватель перечисленных спутников планеты Юпитер). 24. Девиз (традиционная геральдическая деталь). 25. «Милая» (романс, отрывок из которого приведен).