Оценка эффективности карантинных мер: что дает математическое моделирование?
В Москве и других регионах России постепенно вводят разнообразные меры, направленные на сдерживание и подавление распространения коронавирусной инфекции: режим самоизоляции, пропускной режим. Какова эффективность этих мер, нужно ли вводить другие или, наоборот, можно начать ослабление режима? Когда ожидать снижение численности заболевающих ежедневно, достижения пика, выхода на плато? В поиске ответов на эти вопросы кандидат химических наук Сергей Ильин из Института нефтехимического синтеза им. А. В. Топчиева РАН предлагает свою математическую модель.
Первые математические модели для прогнозирования развития инфекционных заболеваний появились в начале XX века. В 1927 году Кермак и Маккендрик предложили для проведения расчетов использовать дифференциальные уравнения с разделением человеческой популяции на людей, восприимчивых к болезни (S), и тех, что уже переболели (R).
Восприимчивые заражались с некоторой скоростью передачи болезни, становясь инфицированными (I), которые в свою очередь поправлялись с некоторой скоростью. Их модель стала известна под аббревиатурой SIR, что отражало одновременный расчет в модели числа восприимчивых, инфицированных и поправившихся персон.
Эта модель послужила основой для развития последующих моделей посредством вносимых модификаций, которые заключались в изменении уравнений или добавлении к расчету других лиц, не относящихся к трем указанным базовым категориям, что позволяло учитывать особенности тех или иных заболеваний. Были разработаны модели, принимающие во внимание возможность повторного инфицирования (модель SIS), смерти (SIRD), наличия у заболевания инкубационного периода (SEIR), временного иммунитета детей благодаря антителам матери (MSIR), повторного инфицирования и наличия инкубационного периода (SEIS) и т.д.
При появлении новой инфекции не известны ни набор категорий лиц, которые необходимо учитывать в модели, ни скорости перехода людей из одной категории в другую. Имеющаяся информация об особенностях новой коронавирусной инфекции COVID-19 и то, как люди ее воспринимают и действуют, должны служить базой для построения модели.
Следует учитывать два фактора: во-первых, наличие длительного инкубационного периода, во время которого носитель инфекции заразен для окружающих, а во-вторых, изолирование выявленных носителей инфекции, которые в результате становятся условно незаразными. Сочетание этих двух факторов делают новую коронавирусную инфекцию уникальной. Обычно всё наоборот: носитель инфекции не опасен для окружающих во время инкубационного периода и становится заразным после его истечения. По этой причине для прогнозирования распространения коронавирусной инфекции необходима новая модель, учитывающие эти обстоятельства.
К сожалению, на настоящий момент неизвестны ни длительность вырабатываемого иммунитета после выздоровления от коронавируса, ни его стойкость. Также еще слишком мало информации для корректного расчета скорости выздоровления больных: небольшой процент популяции поправляется буквально спустя неделю после инфицирования, тогда как основная масса долго и продолжительно болеет. Поэтому предложенная модель не окончательна, но может быть полезна для составления прогноза и принятия управленческих решений.
Ключевым является разделение всех заболевших на две группы: выявленных и затем изолированных носителей инфекции (ND) и тех, которые остаются невыявленными в силу не прошедшего у них инкубационного периода и продолжают распространять заболевание в популяции (NA). Общее число заболевших (NT) на некоторую дату di равно сумме выявленных и невыявленных носителей инфекции на ту же дату:
NT(di) = ND(di) + NA(di). (1)
Средний инкубационный период (tD) заболевания равен шести дням, поэтому, в среднем, каждый заболевший спустя шесть дней после инфицирования обращается за помощью и изолируется, т.е. общее число выявленных носителей инфекции на дату di равно общему числу заболевших шестью днями ранее:
ND(di) = NT(di-6). (2)
Каждый день число инфицированных возрастает. Болезнь разносят невыявленные носители инфекции с некоторой скоростью, которую характеризует параметр, называемый трансмиссивностью (R0). Численно параметр равен среднему числу людей, которое заражает один человек до изоляции, и зависит от плотности и поведения населения на разных этапах развития эпидемии. При R0 меньше 1.0 эпидемия затухает, и наоборот.
В среднем невыявленный больной распространяет инфекцию в течение шести дней. Это значит, что в день он заражает R0/6 человек. Кроме того, будем считать, что у переболевших вырабатывается стойкий иммунитет, исключающий повторную возможность их инфицирования. Тогда общее число заразившихся на дату di равно сумме общего числа зараженных днем ранее и числа новых зараженных, которое пропорционально числу еще невыявленных зараженных с учетом трансмиссивности болезни и доли уже ранее заразившегося населения:
NT(di) = NT(di-1) + R0×NA(di-1)×(1-NT(di-1)/NP)/6, (3)
где NP – общее население страны или города.
На момент начала эпидемии (дату d0) NA(d0)=1, NT(d0)=1, а ND(d0)=0. Таким образом, для каждого последующего дня можно рассчитать общее число зараженных по уравнению (3), общее число уже выявленных больных по уравнению (2), а затем и общее число пока невыявленных зараженных по уравнению (1).
Данные уравнения представлены в дискретной, а не дифференциальной (непрерывной) форме, благодаря чему для проведения расчетов данную модель легко воспроизвести в любом редакторе электронных таблиц, например, Microsoft Excel.
На первый взгляд кажется, что модель не учитывает существования бессимптомных носителей инфекции, но это не так: поскольку доля бессимптомных носителей в популяции с течением времени не изменяется, их наличие учитывается неявным образом величиной коэффициента R0. При этом в случае изменения поведения населения с даты d1 (например, из-за введения или пересмотра карантинных мер) параметр R0 меняет с этой даты свое значение, становясь R1. Если далее поведение снова изменяется, то появляется пара d2 и R2 и т.д.
Данная модель была протестирована на исторических данных о заболеваемости в восьми странах: КНР, Италии, Испании, США, Великобритании, Японии, Франции и Германии (рис. 1). Для всех стран на начальном этапе эпидемии трансмиссивность вируса лежала в пределах 2.28–3.12, причем наибольшее значение параметра было характерно для Китая, в котором один человек заражал трех, вероятно, из-за более высокой плотности населения. Введение и последовательное усиление карантинных мер приводило к снижению трансмиссивности вируса, что было заметно спустя шесть дней по снижению скорости прироста числа новых случаев заболевания.
Все страны вводили меры постепенно. Первоначальные ограничения приводили к снижению трансмиссивности вируса до значения 1.20–1.74, что было недостаточно (нужно добиться трансмиссивности меньше единицы) и вирус продолжал распространяться с ускорением. В результате все рассмотренные страны, за исключением Японии, пошли на ужесточение мер, обеспечив снижение трансмиссивности до 0.87–1.14.
Япония сделала ставку на своевременное выявление и изолирование зараженных. Можно заключить, что данная стратегия не работает: кривая числа заболевших для Японии то замедляет свой ход, то вновь ускоряется. Это результат того, что Японии удается успешно изолировать большинство зараженных, но несколько человек (достаточно одного!) остаются неизолированными и вновь начинают развитие эпидемии.
Китай, напротив, пошел на дальнейшее усиление мер, вплоть до запрета выходить за покупками чаще одного раза в три дня и то, только одному представителю семьи, проживающей вместе, а также строгой фиксации всех перемещений и контактов между гражданами. Это привело к снижению показателя трансмиссивности до 0.36 и быстрой победе над эпидемией (за 6 недель согласно расчетам по модели).
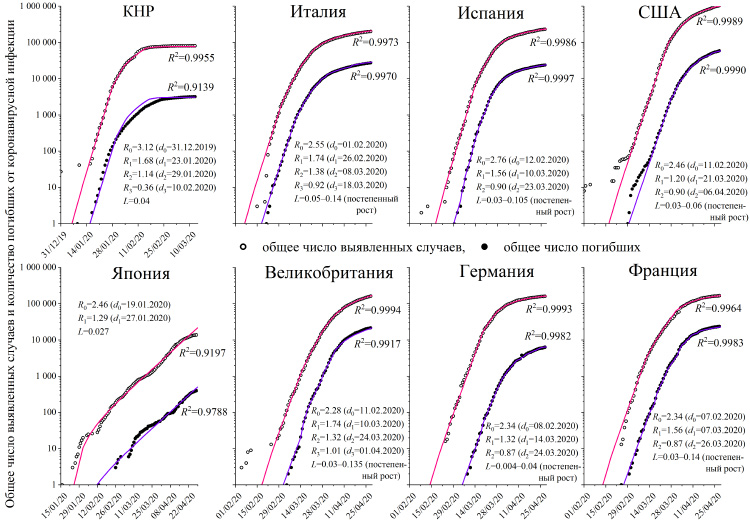
Рис. 1 Общее число выявленных случаев (полые точки) и количество погибших (зачерненные точки) от коронавирусной инфекции в некоторых странах. Параметры модели приведены у кривых, у которых также показано значение коэффициента детерминации (R2), который тем ближе к 1.0, чем лучше модель описывает экспериментальные данные; при R2>0.8 модель можно считать хорошо работающей.
При этом следует понимать, что любое облегчение карантинных мер приведет к росту трансмиссивности и возобновлению ускоренного распространения вируса. Чтобы этого не случилось после снятия карантинных ограничений, трансмиссивность вируса должна оставаться меньше единицы. Например, в случае Италии изначальная трансмиссивность была равной 2.55, поэтому, чтобы она оставалась меньше единицы при отмене карантина, необходимо, чтобы 61 % населения Италии или переболел, или был вакцинирован (при условии стойкости и долговременности вырабатываемого иммунитета).
В настоящий момент согласно официальной статистике болеет или уже переболело 0.33 % населения Италии. Статистика не учитывает бессимптомные и легкие варианты протекания болезни, которые, пока только по слухам, могут превышать числом официально регистрируемые случаи в 4–50 раз.
Однако даже если это действительно так, процент переболевших всё равно оказывается существенно ниже необходимого: снятие карантина неизбежно приведет к возвращению скорости роста числа инфицированных практически на первоначальный уровень. Иными словами, скорая разработка вакцины является жизненно необходимой для победы над заболеванием в обозримые сроки.
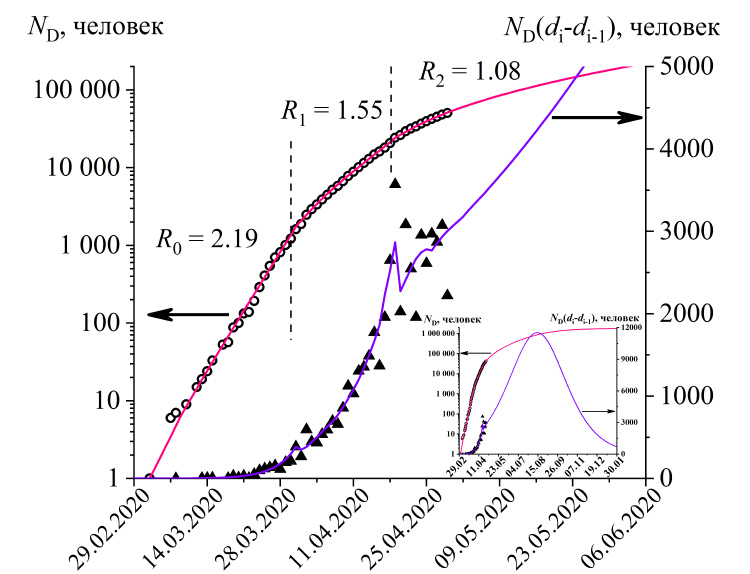
Рис. 2 Общее число выявленных случаев (полые точки) и новые выявленные случаи (зачерненные точки) коронавирусной инфекции в городе Москве. Линиями показаны расчеты согласно модели (R2=0.9998). На вкладке показаны те же данные, но для большего периода времени. Параметры модели: R0=2.19 (d0=22.02.2020), R1=1.55 (d1=25.03.2020), R2=1.08 (d1=13.04.2020).
Теперь применим модель для анализа параметров распространения инфекции в городе Москве (рис.2) и в среднем по России (рис.3). На начальном этапе развития эпидемии трансмиссивность коронавируса составляла в среднем по России 2.1, т.е. один зараженный инфицировал в среднем чуть больше двух человек. В Москве этот параметр был немного выше (R = 2.19), вероятно, из-за большей плотности населения.
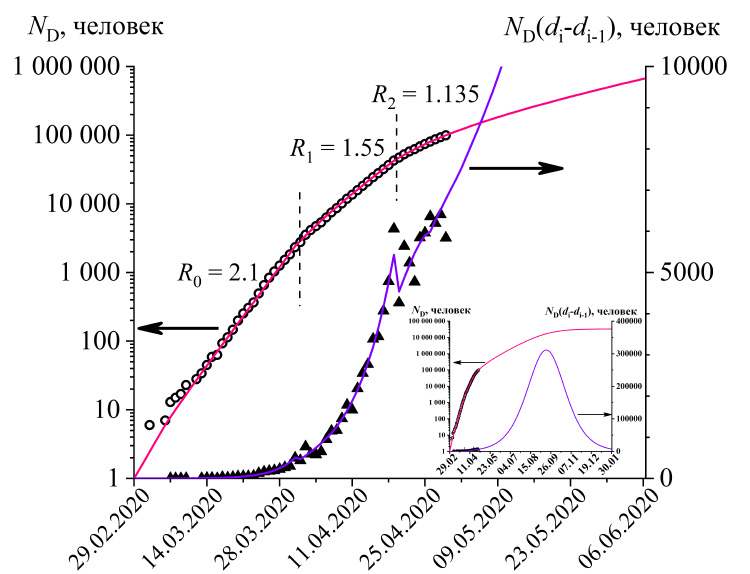
Рис 3. Общее число выявленных случаев (полые точки) и новые выявленные случаи (зачерненные точки) коронавирусной инфекции в России. Линиями показаны расчеты согласно модели (R2=0.9999). На вкладке показаны те же данные, но для большего периода времени. Параметры модели: R0=2.1 (d0=22.02.2020), R1=1.55 (d1=25.03.2020), R2=1.135 (d1=13.04.2020).
Введение режима самоизоляции в Москве и других регионах России привело к снижению трансмиссивности вируса до одинаковой величины 1.55, таким образом не остановив развитие эпидемии. Ответом стало введение пропускного режима в Москве и некоторых других регионах. В результате трансмиссивность в Москве упала до 1.08, т.е. в два раза, по сравнению с исходной величиной R0. Тем не менее, величина всё еще больше единицы, что означает продолжение ускоренного распространение коронавируса среди горожан. Поскольку пропускной режим действует не во всех регионах, то в целом по России трансмиссивность оказывается выше, чем по Москве, равной 1.135.
С практической точки зрения, при прочих равных условиях, т.е. при сохранении текущих карантинных мер, достижение пикового значения числа выявленных заболевших за день будет достигнуто на второй неделе августа в случае Москвы (11500 новых случаев), и в середине сентября в целом по России (310000 новых случаев).
После прохождения пика потребуется еще много месяцев на то, чтобы число новых выявляемых случаев заболевания снизилось до приемлемого уровня. Например, по Москве число новых случаев снизится до 1000 в день только в январе 2021 года (см. вкладки к рис. 2 и 3). В итоге к концу эпидемии заразится 15-23% популяции.
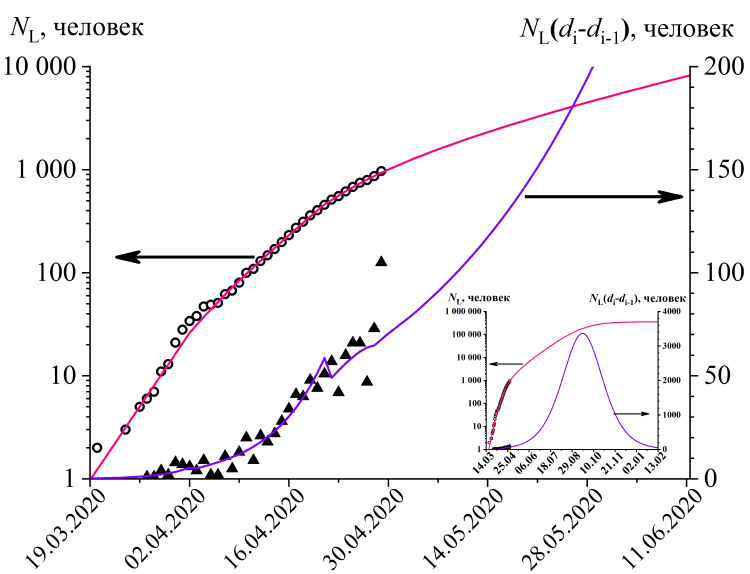
Рис.4. Общее число погибших (полые точки) и новые случаи гибели (зачерненные точки) от коронавирусной инфекции в России. Линиями показаны расчеты согласно модели (R2=0.9991). На вкладке показаны те же данные, но для большего периода времени. Параметры модели: tL=8, L=0.0108, остальные параметры такие же, как приведенные для рис 3.
Модель позволяет оценить возможное число жертв эпидемии (рис 4). Общее число погибших на дату di равно общему числу заболевших несколькими днями ранее, помноженному на летальность:
NL(ti) = NT(di-tL)×L, (4)
где tL – среднее время от заражения до смертельного исхода, найдено равным 8 дням, и L – летальность, равная отношению числа погибших к сумме количеств погибших и выздоровевших, найдена для России равной 1.08%.
Для других стран летальность лежит в пределах от 0.4 до 14 % и в большинстве случаев возрастает по мере развития эпидемии (см. рис. 1). При этом следует понимать, что рассчитанная величина летальности является завышенной, причем тем сильнее, чем меньше выявляется бессимптомных и легких случаев протекания болезни.
При сохранении текущих условий пиковое число смертей в России придется на середину сентября (3300 погибших в сутки), а общее число потерь может достигнуть 360 тысяч человек (см. вкладку к рис. 4).
Подобного негативного сценария можно избежать, усилив карантинные меры и снизив тем самым трансмиссивность вируса ниже 1.0. В таком случае пик заболеваемости будет достигнут спустя шесть дней, а последующая скорость снижения выявления новых случаев болезни будет тем выше, чем ниже будет показатель трансмиссивности, т.е. чем более жёсткими будут принятые меры.
Таблица 1. Прогноз общего числа заболевших и погибших от коронавирусной инфекции согласно модели.
|
Дата* |
Общее число выявленных случаев |
Общее число погибших |
|
|
Москва |
Россия |
||
|
30.04.2020 |
54256 |
106913 |
1005 |
|
01.05.2020 |
57376 |
114190 |
1079 |
|
02.05.2020 |
60555 |
121728 |
1155 |
|
03.05.2020 |
63806 |
129557 |
1233 |
|
04.05.2020 |
67128 |
137682 |
1315 |
|
05.05.2020 |
70518 |
146107 |
1399 |
|
06.05.2020 |
73976 |
154843 |
1487 |
|
07.05.2020 |
77504 |
163900 |
1578 |
|
08.05.2020 |
81103 |
173292 |
1672 |
|
09.05.2020 |
84777 |
183035 |
1770 |
|
10.05.2020 |
88525 |
193138 |
1872 |
|
11.05.2020 |
92347 |
203615 |
1977 |
|
12.05.2020 |
96246 |
214478 |
2086 |
|
13.05.2020 |
100222 |
225742 |
2199 |
*данные на 11 утра.
В рассчитанные с помощью модели данные трудно поверить. Лучшим и единственным критерием работоспособности какой-либо теории является ее способность точно предсказывать будущее. В Таблице 1 приведен прогноз на ближайшие две недели.
Препринт работы доступен на сайте MedRxiv



