Суть этой геометрической задачи заключается в отыскании графического метода деления произвольного угла на три равные части с помощью циркуля и обыкновенной линейки. Ниже приводим описание метода, решающего эту задачу независимо от размера и типа (острый, тупой) угла, предлагаемого для разделения. Ограничений на формы геометрических фигур нет, численных измерений или вычислений не делается. Для примера взят случайный угол.
Геометрические элементы комбинируются геометрической фигурой, состоящей из равнобедренного треугольника АВС с нижним углом В, подлежащим разделению на три равных угла, и равносторонней трапеции АDFC, все четыре угла которой находятся на равном расстоянии от вершины угла В. Треугольник и трапеция сомкнуты своими основаниями АС. Предлагаемый метод решения задачи состоит в следующем:
1) Основанием для построения упомянутой геометрической фигуры служат уравнения, связывающие основные ее элементы:
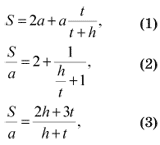
где S - основание треугольника и трапеции; а - сторона трапеции; t - высота треугольника; h - высота трапеции.
Главные элементы фигуры находятся во взаимной зависимости: отношения основания к стороне трапеции и высот трапеции треугольника связаны уравнением (2).
У отношений S/а и h/t есть пределы применимости: отношение основания трапеции к ее стороне находится в пределах 2 ... 3, а отношения высот трапеции и треугольника изменяются при этом от бесконечности до 0. За пределами этих ограничений построение фигуры треугольник плюс трапеция невозможно.
В таблице для примера и выбора основных показателей для построения треугольника и трапеции приведены некоторые численные значения переменных, входящих в уравнения. С ее помощью можно задать отношение S/а и получить отношение h/t.
На рис. 1 представлено решение задачи предлагаемым методом. В качестве примера, не имеющего принципиального значения, взято равенство высот треугольника и трапеции. Для большей наглядности на рисунке приведены дополнительные геометрические построения: деление угла надвое, проведение параллельных линий и нанесение равномерных делений.
Решение задачи начинается с деления заданного угла АВС пополам линией ВЕ и проведения под прямым углом к ней через точку В горизонтальной линии XY. На линии ХY в обе стороны от точки В наносятся деления, отвечающие отношению основания трапеции к ее стороне, в данном случае 5 и 2. Это соотношение получено из уравнения (2) при условии равенства высот - см. таблицу.
Из точек, отвечающих делению 5, проводятся параллели биссектрисе ВЕ до пересечения со сторонами угла в точках А и С. Линия АС служит общим основанием треугольника и трапеции, отрезки АВ и ВС равны. Из точек, отвечающих отметке 2 на отрезке XY, проводятся линии, также параллельные биссектрисе угла АВС, и на них отрезками BD и BF, равными сторонам треугольника ВА = ВС, отмечаются точки D и F - вершины углов трапеции АDFC. Точки D и F определяют высоту ВЕ, равную сумме высот треугольника и трапеции.
Для проверки и доказательства проводятся диагонали AF и DC трапеции АDFC, пересекающиеся в точке Z на средней линии треугольника АВС. Образовавшиеся два треугольника АDF и DFC равнобедренные, поскольку их основания, т. е. диагонали трапеции, разделены в точках Т надвое, пересекаясь в них с радиусами ВD и ВF и средней линией РР трапеции. Сторона DF принадлежит обоим треугольникам, поэтому треугольники АВD, DВF и FВС равны. Все три их угла с вершинами в точке В равны между собой и в сумме составляют заданный угол АВС.
Отрезки прямых DM и FN образуют стороны ромбов ADFN и DFCM, своими геометрическими свойствами подтверждающих правильность построения.
На рис. 2 показано соотношение образовавшихся углов. Характерно, что нижние углы трапеции DАС = FСА равны одной трети разделяемого угла АВС.
При построении геометрической фигуры на рис. 1 было принято отношение величины основания трапеции к ее стороне 5:2 для простоты построений: этому соотношению отвечает равенство высот трапеции и треугольника.
На рис. 3 построена фигура "треугольник - трапеция" для сравнительно острого угла АВС. Исходным принимается отношение высоты треугольника к сумме высот треугольника и трапеции, равное 5:6, которому, согласно уравнению (1), отвечает значение S/а = 17/6. Как и в первом случае, это значение поровну, т. е. 8 1/2 к 3, откладывается на линии XY в обе стороны от точки В, и производятся аналогичные построения.
Вообще, нет необходимости предварительно принимать численные значения S/а. Достаточно на линиях ВХ и ВY из точки В отложить по три равных отрезка, отметив их концы, и из любой точки между второй и третьей отметками построить перпендикуляры до пересечения со сторонами угла В в точках А и С. Затем из первой отметки также восстановить перпендикуляры и на них отложить точки D и F на расстоянии от точки В, равном стороне треугольника АВС.
Если из точек А и С на линиях ВD и ВF отложить по две равноотстоящие точки N и М, получим отрезок NM, равный S-2а. Отношение этой длины к а определяет отношение высот трапеции и треугольника согласно формуле (2).
В остальном поступают, как и в первом случае. Правильность построения можно проверить по формуле
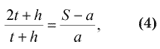
следующей из (2). Сумма t+h никогда не превышает сторону ВА(ВD) треугольника.
Графически равенство (4) проверяется так (рис. 4). Берется произвольный угол PQN, разделенный биссектрисой QQ?. На левой стороне угла от точки Q циркулем откладываются отрезки S-а и а, образующие точки Р и L. Далее точка Р соединяется с точкой Q? и из точки L проводится параллельная РQ? линия LQ???. Это означает, что на биссектрисе угла возникла отметка Q, причем а/(S-а)= = QQ??/QQ?. На правой стороне угла откладываем циркулем отрезки 2t+h и t+h из построенного чертежа. Конец отрезка 2t+h - точку N - также соединяем с точкой Q?, а из точки М - конца отрезка t+h - проводим линию, параллельную NQ?. На средней линии угла отмечается отношение (t+h)/(2t+h)=QQ??? /QQ?. Если линии LQ?? и МQ??? пересекаются на средней линии угла, это означает, что левая и правая части в формуле равны. Что и требуется.
Можно ли путем измерения соответствующих отрезков, в частности оснований треугольников, определить их длину? Нельзя, так как каждый служит хордой соответствующей воображаемой дуги окружности, содержащей долю, не поддающуюся измерению. Для определения точности решения задачи может быть использован только графический метод.
Таким образом, нами предложено доказательство возможности графического деления угла на три с помощью циркуля и линейки. Остается графически не выясненной связь элементов трапеции и треугольников, иными словами, зависимость между стороной трапеции а и высотой треугольника t. Эта задача может иметь самостоятельный характер для принципа построения трапеции.
Приношу благодарность профессору МГТУ В. И. Солонину за благожелательную критику.




