Вопрос кажется странным, ведь кожура — это тонкий слой, край апельсина (будем считать, что апельсин имеет форму шара). Оказывается, что относительно тонкий слой на границе шара имеет тот же объём, что и вся остальная часть. Например, у апельсина диаметром 10 см с кожурой толщиной 1 см почти половина всего объёма сосредоточена в кожуре!
Давайте проверим. Рассмотрим два шара радиусов R и r (r<R). Каким должен быть радиус меньшего шара, чтобы его объём составлял половину объёма большого?
Объём шара радиуса R равен
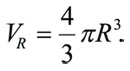
Для нахождения r запишем уравнение:
Vr = VR − Vr или
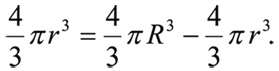
Отсюда следует, что R3 = 2r3, то есть
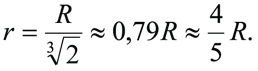
Таким образом, почти половина объёма шара сосредоточена в слое около поверхности толщиной всего лишь 1/5 радиуса, а в апельсине, представленном на рисунке, кожуры и мякоти поровну.
Поясним выбор формы уравнения Vr = VR − Vr вместо естественного VR = 2Vr. Это сделано, чтобы напомнить одну идею, часто встречающуюся в геометрии и полезную при решении житейских задач — фигура, для площади или объёма которой нет готовой формулы, представляется как разность «известных» фигур.




