- А вот и Лестрейд, - произнес Холмс, услышав мелодичный звон дверного колокольчика.
- Почему вы так думаете? - отозвался Уотсон.
- Элементарно, я только что просмотрел утренние газеты, и все они пестрят заголовками о вчерашнем злодейском убийстве в пригороде Лондона и о бессилии полиции найти преступника.
И действительно - не успел Холмс закончить, как появился хмурый озабоченный сыщик Скотленд-ярда Лестрейд.
- Как дела? - после взаимных приветствий спросил Холмс. - Нашли преступника?
Лестрейд молча кивнул, но фигура его при этом как-то поникла. Он вспомнил недавний разговор с начальником полиции. В его ушах все еще звучал шипящий, прерывающийся от злобы голос шефа, потрясающего перед его носом пачкой газет:
- Где преступник? Если в течение трех дней вы его не найдете, будете работать не сыщиком, а конюхом в Скотленд-ярде!
После недолгих колебаний Лестрейд решился обратиться к Шерлоку Холмсу.
- Холмс, я никогда не сталкивался с подобным преступлением: преступник есть и его нет!
- Как это понять? - воскликнул Холмс. - Поясните, дружище, что вы этим хотите сказать.
- Преступника я нашел, абсолютно уверен, что это он, но ничего доказать не могу, а вы знаете: нет доказательств, и преступник уже не преступник.
Уотсон молча слушал, изредка наблюдая за Холмсом. И видя, с каким вниманием тот слушал сыщика, понял, что дело, которое не по зубам даже такой ищейке, как Лестрейд, заинтересовало его. Так и оказалось. Холмс поудобнее устроился в кресле и произнес:
- Рассказывайте, Лестрейд, я весь во внимании.
- Дело вроде бы и несложное, но я буду рад вашему участию. Вчера на полустанке в 23 милях от Лондона была убита графиня мисс Джеми Хадсон. Невольным свидетелем произошедшего оказался старый сторож, который убирал платформу. Мисс Хадсон около 11 часов утра сошла с поезда и присела на лавочку в ожидании автомобиля, который должен был ее встретить. В это время к ней подошел бородатый молодой человек в сильно надвинутой на глаза кепи и попытался выхватить сумочку. Старая графиня оказала отчаянное сопротивление и подняла крик. Тогда грабитель выстрелил в нее, схватил сумочку и быстро исчез в густых зарослях кустарника, окружающего полустанок. Сторож слышал и шум отъезжающего автомобиля.
Мисс Хадсон ехала к племяннику сэру Чарльзу Чейни. Зная его пристрастие к карточной игре и беспутный образ жизни, она неоднократно предупреждала, что перепишет завещание, по которому племяннику отходило крупное состояние, и сделает его нищим. Вчера графиня решилась на последний разговор.
По подозрению в убийстве задержан сэр Чарльз. Ограбление же на полустанке я, Холмс, рассматриваю как инсценировку, как попытку пустить следствие по ложному пути: убедить меня на основании показаний сторожа искать бородатого грабителя. Но я хорошо усвоил старое правило: если хочешь раскрыть преступление - ищи того, кому оно выгодно. Поэтому я в первую очередь арестовал сэра Чарльза и не собираюсь гоняться за мифическим преступником в кепи.
- Так, - протянул Холмс, - мотив убийства налицо, а как насчет возможности?
- В этом-то все и дело, - вздохнул Лестрейд, - мотив у сэра Чарльза есть, а возможности нет!
- А нет ли других подозреваемых?
- Исключено. Старая графиня отличалась большой добротой и высокой порядочностью. Все, кто знал ее, относились к ней с большой любовью, и весть об ее убийстве всколыхнула Лондон, а начальник полиции пообещал выгнать меня с работы, если не найду преступника и не представлю убедительных доказательств. Но, несмотря на все наши старания, мы не смогли найти никаких улик.
- Нет ли алиби у сэра Чарльза?
- И да и нет! В этот день, как обычно, с раннего утра у сэра Чарльза собралась компания. Ровно в 9 часов 10 минут он сообщил, что отправляется на автомобиле на полустанок за мисс Хадсон. В 12.54 он вернулся (это время запомнил один из гостей, который поинтересовался, как долго отсутствовал сэр Чарльз), объяснив, что недалеко от дома у него испортился автомобиль и он был вынужден вернуться обратно. Так что сэр Чарльз отсутствовал 3 часа 44 минуты, с 9.10 до 12.54, то есть в момент убийства графини.
Но все дело, Холмс, в том, что за это время - 3 часа 44 минуты - доехать от фермы до полустанка и вернуться невозможно.
- Так, - задумчиво произнес Холмс. - Уотсон, будьте любезны, дайте лист чистой бумаги и карандаш Лестрейду, и пусть он нарисует нам чертеж местности.
- Хорошо, - отозвался Лестрейд и быстро изобразил, давая пояснения, план местности.
- Точки О и А обозначают дом сэра Чарльза и полустанок. Расстояние между ними 49,9 мили. Вдоль железной дороги тянется узкая лесополоса. В ней проходит плотная ровная дорога. Вокруг дома до самой лесополосы простирается скошенное поле.
Глядя внимательно на чертеж, Холмс спросил:
- Лейстрейд, когда проводили следственный эксперимент, проверяя, можно ли за 3 часа 44 минуты добраться от дома сэра Чарльза до полустанка и вернуться, по какой дороге ехали?
- Как по какой? - удивился Лестрейд. - Разумеется, по самой короткой: по прямой ОА. Наибольшая скорость автомобиля на ней - 24,8 мили в час.
- Уотсон, - произнес Холмс, - будьте любезны, дайте мне карту местности и книгу в зеленом сафьяновом переплете со второй полки.
Подавая карту и книгу, Уотсон мельком взглянул на нее - книга была по математике. Но ничего не спросил и молча опустился обратно в кресло.
Тем временем Холмс достал из стола измерительную линейку, остро отточенный карандаш и склонился над картой.
Уотсон и Лестрейд внимательно следили за ним.
Холмс провел несколько прямых на карте, измерил по ней какие-то расстояния и углубился в длительные расчеты, изредка заглядывая в книгу.
Прошло немало времени, прежде чем Холмс оторвал взгляд от стола и воскликнул:
- Наконец-то закончил!
И обращаясь уже к Лестрейду, продолжил:
- Нет преступления, не оставляющего улик. Надо только знать, где их искать, и уметь найти. Где искать, я вам сообщу: в перелеске, около железной дороги, в 23 милях от полустанка, а найти улики уже ваше дело.
Лестрейд вскочил:
- Будьте уверены, Холмс, если улики там, я их найду!
И действительно, на следующий день вечером в квартиру Шерлока Холмса ворвался Лестрейд. Он был в сильном возбуждении. И лицо его так и светилось счастьем.
- Нашел улики, - с порога крикнул он, - именно там, где вы, Холмс, указали! Я нашел следы протектора автомобиля сэра Чарльза. И время движения по пути, указанному вами - от дома по полю до этого места в перелеске, затем по дороге до полустанка и обратно, - составило 3 часа 42 минуты. Так что, Холмс, благодаря вам я теперь имею неоспоримые улики против сэра Чарльза. Дело можно считать закрытым.
Дорогой Холмс, - продолжал самодовольно Лестрейд, - хотя я не разделяю ваших методов, но должен признать, что ваша интуиция позволяет иногда самым удивительным образом разгадывать преступления. Если бы вы еще к тому же уделяли больше внимания практике, как я, то действительно могли стать хорошим сыщиком.
- Благодарю вас, Лестрейд, - усмехнулся Холмс, - за комплимент и добрый совет, я непременно последую ему.
Поздно вечером, когда Лестрейд ушел и Холмс расположился в своем кресле возле камина, Уотсон решился наконец спросить друга:
- Холмс, как вы определили место, где надо было искать улики?
- Элементарно! В одном Лестрейд прав: преступление на редкость дерзкое, расчет преступника был в том, что сыщики Скотленд-ярда действуют прямолинейно, для них самый короткий путь - это движение по прямой. Вот и Лестрейд считал, что преступник двигался по кратчайшему пути ОА от фермы до полустанка.
- Холмс, - не удержался Уотсон, - но путь по прямой действительно наикратчайший!
- Нет, дорогой Уотсон. Путь по прямой - самый короткий по расстоянию, но не по времени движения. Посмотрите на карту, Уотсон: преступник мог двигаться от дома до полустанка и по другому пути - доехать сначала до дороги в лесополосе, а затем по ней добраться до полустанка. В отличие от Лестрейда это хорошо понимал сэр Чарльз и выбрал именно такой путь.
- Значит, Холмс, кривой путь оказался короче! Но как вы это установили?
- Сейчас объясню. Вот, Уотсон, чертеж Лестрейда. На нем через точку А, изображающую полустанок, проведем прямую вдоль железной дороги. Она изобразит дорогу в лесополосе. Теперь из точки О, обозначающей дом, опустим перпендикуляр на прямую в точку С и начертим отрезок ОD (см. рис. 1.).
В результате получим схему возможных путей от дома до полустанка.
- Холмс, а не мог ли сэр Чарльз двигаться по какому-то другому пути?
- Нет, Уотсон, все остальные пути от дома до полустанка, как видно из чертежа, заведомо хуже.
Пусть t , - продолжал далее Холмс, - время движения по пути ОDА. Как видно из чертежа, он зависит от угла СОD, который обозначим φ, и, следовательно, t = t(φ). Определим зависимость t от φ. Для этого построим систему координат, проведя одну ось через точку О параллельно прямой АС, а другую - перпендикулярно ей. Назовем одну из них Oφ, на ней будем откладывать углы φ, другую - Ot, на этой оси откладываем значения t(φ).
- Так, - произнес Уотсон, глядя на чертеж, - теперь я начинаю понимать. Вы, Холмс, хотите найти зависимость времени от угла φ. Затем определить угол φопт, при котором время движения минимально. И, зная этот угол, отыщите путь, по которому двигался преступник.
- Браво, Уотсон! Вы делаете успехи!
- Стараюсь, Холмс! Но как вы получили зависимость времени движения от величины угла φ?
- Элементарно! По карте вычислил кратчайшее расстояние между домом и дорогой, то есть расстояние ОС. Оно оказалось равным
OC = h = 29,7 мили.
Из прямоугольного треугольника ОСD нашел расстояние ОD:
OD = h/cosφ =29,7/cosφ.
Скорость движения автомобиля по скошенному полю, как установил Лестрейд, равна v =24,8 мили в час. Поэтому на путь ОD затрачивается
h/v . cosφ.
Далее по карте определил расстояние СА:
CA = H = 40,1 мили.
Из треугольника ОСD - расстояние СD:
CD = h tg φ = 29,7 tg φ мили
и нашел длину пути DА:
DA = CA - CD = H - h tgφ = 40,1 - 29,7 tgφмили.
По утверждению Лестрейда, дорога DА ровная и плотная, поэтому по этой дороге автомобиль может развить максимальную скорость. Для автомобиля сэра Чарльза она составляет, насколько мне известно, υ = 49,7 мили в час. Следовательно, на путь DА затрачивается
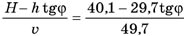часов.
И, таким образом, время движения от дома до полустанка по пути ОDА
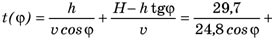
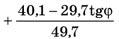часов.
Итак, Уотсон, функция t(φ) получена. Установим теперь угол φопт, при котором время t(φ) минимальное. Для этого воспользуемся методом спуска.
- Холмс, - взмолился Уотсон, - в чем его суть?
- По методу спуска выбираем начальное значение угла φ, например φ1 = 0о, и определяем некоторое число ∆φ1 > 0, например ∆φ1 = 1о, такое, что t(φ1 + ∆φ1) < t(φ1). Затем, полагая последовательно k =2, 3, ... в неравенстве
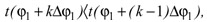
находим первое значение k = k*, при котором оно нарушается, то есть
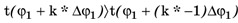
Число φ1 + k* ∆φ1 обозначим φ2 и продолжим спуск таким же образом, но только в обратном направлении, то есть находим положительное число ∆φ2, например
,
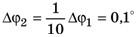при котором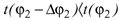 
и так далее. В результате получается последовательность значений φ1, φ2 ... , приближающихся к углу φопт. Так, после некоторого n-ного шага можно получить приближенное значение φnугла φопт..
- Холмс, - спросил Уотсон, - но как вы определите, что найденное значение угла - действительно приближенное значение φопт?
- Очень просто! Из метода спуска следует, что угол φопт находится между углами φn и φn-1. Поэтому погрешность |φn - φопт| не превысит |φn - φn-1|, то есть |φn - φопт| ≤|φn - φn-1|.
Продолжим, Уотсон. Используя этот метод спуска, за три шага я вычислил приближенное значение φ4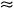 
30о угла φопт, и, следовательно, наименьшее время, за которое можно добраться от дома до полустанка, t(φопт) 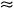t(30о) = 1 час 42 минуты. .
Таким образом, сэр Чарльз вполне успевал за 3 часа 44 минуты доехать от дома до полустанка и вернуться обратно. Поэтому я и посоветовал Лестрейду искать улики именно около лесополосы, в 23 милях от полустанка. С чем он великолепно справился.
- Холмс, - спросил Уотсон, - нет ли более простых методов отыскания минимального значения функции t(φ)?
- Есть, но они требуют знания уже высшей математики, в частности производной...
- Не надо, Холмс, - прервал его Уотсон, - все же я доктор, а не инженер! Лучше ответьте: где еще приходится иметь дело с отысканием оптимальных решений?
- Дорогой Уотсон! Вся наша жизнь - это непрерывная цепь попыток найти оптимальные решения тех или иных вопросов, с которыми приходится сталкиваться повседневно в жизни! На практике же потребность в отыскании оптимальных решений возникает при отыскании лучших путей перевозки грузов, в задачах о том, как раскроить материал, чтобы отходы были минимальными, и во многих других случаях.
Ну вот и все, - продолжал Холмс. - Это дело доставило мне большое удовлетворение: я встретился с равным противником, обладающим аналитическим умом. Логика его преступления основывалась на том, что сыщики Скотленд-ярда, ярким представителем которых является Лестрейд, отличные ищейки, имеющие бульдожью хватку, но абсолютно не в ладах с логическими методами и тем более с математическими, и поэтому сэр Чарльз был уверен, что Лестрейд никогда не определит оптимальный путь и, не зная его, не сможет найти место, где следует искать улики. Искать же на площади почти в 600 квадратных миль дело явно безнадежное. Так что, дорогой Уотсон, если у вас не осталось больше вопросов, то, будьте добры, подайте мне скрипку.
