№05 2015
|
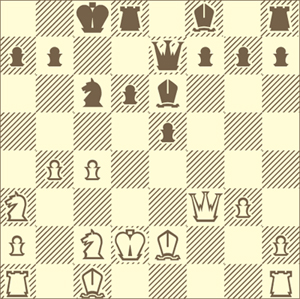
Миниатюры Магнуса Карлсена
В течение довольно длительного времени на страницах «Науки и жизни» мы рассказывали о шахматных миниатюрах всех чемпионов мира. |
|
|
|
|
|
№06 2019
|
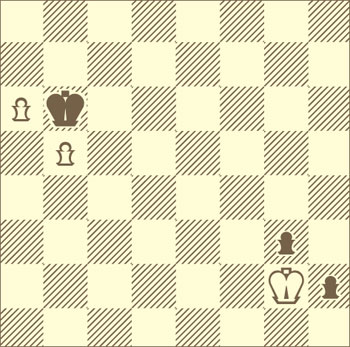
Блуждающий квадрат
Одинокая проходная пешка стремится в ферзи. Её настигает неприятельский король... |
|
№04 2019
|
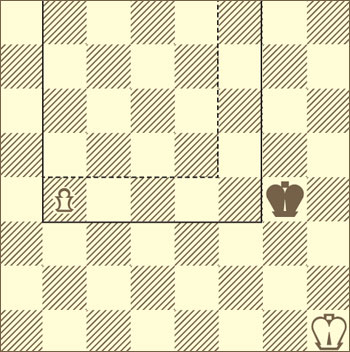
Правило квадрата
Предположим, у одной стороны имеется проходная пешка. А неприятельский король стремится догнать её и съесть. |
|
№02 2019
|
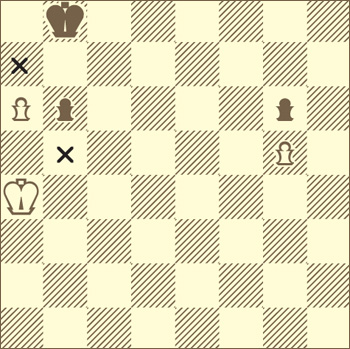
Поля соответствия
Представим такую шахматную картину. Пешечный энд-шпиль, все пешки блокированы, каждый из королей в своём лагере... |
|
№07 2018
|
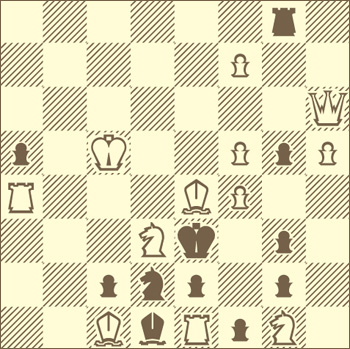
Совершенствуя задачу Бэбсона
Задача сконструировать позицию, где в ответ на превращение чёрной пешки в определённую фигуру следовало бы превращение белой пешки в ту же фигуру, и так четыре раза, занимает умы шахматистов уже почти сто лет |
|
|
|
|
|
|
|
|
|
|
|
|
№12 2016
|
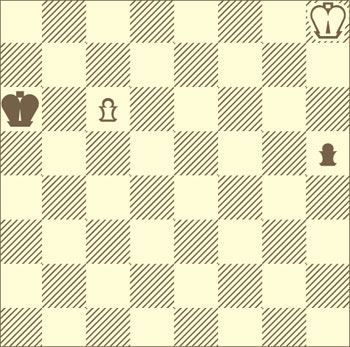
Сорок пешечных квартетов
Решение этюдов — один из лучших способов повысить своё мастерство, развить тактическое зрение, научиться разбираться в окончаниях. |
|
|
|
|

№09 2016
|
Новые малютки
Сколько всего существует различных видов шахматных малюток — этюдов с пятью фигурами на доске? |
|
|
|
|
№06 2016
|
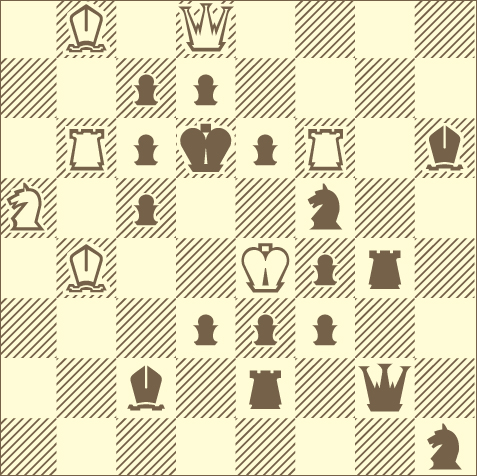
Ещё шестнадцать шуток
Мы предлагаем ещё 16 задач-шуток, которые трудно объединить в одну группу. |
|
|

№04 2016
|
Задачи–шутки на шахматной доске
Появившаяся полвека назад книга «Физики шутят» стала настолько популярной, что шутить начали математики, химики, биологи. Шахматисты не исключение. |
|

№03 2016
|
Марк Тайманов: шахматы, музыка и любовь
Международный гроссмейстер, чемпион СССР, двукратный претендент на звание чемпиона мира, неоднократный олимпийский чемпион в составе сборной страны... |
|
|
№01 2016
|
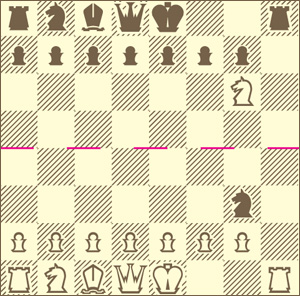
Симметрия и асимметрия на шахматной доске
В нашей рубрике мы не раз сталкивались с мотивами симметрии (и асимметрии!) на шахматной доске, постараемся теперь как можно глубже и полнее осветить эту тему. |
|
|
|