Я порылась в сети что нам предлагает физика для базового представления(Физическая энциклопедия ) и для некоторых частных случаев (Учебник для ВУЗов: Физика открытых информационных систем. Нижегородский государственный университет им. Н.И. Лобачевского 2007 год) и прочитала здешние последние февральские тексты Случайного прохожего
Пока для начала что пишут по фундаментальным и практическим свойствам ВуЗовский учебник еще в названии сообщает
И уже во введении многое для чайников типа меня становится понятным
И когда мы смотрим на флуктуации описанные в Физической энциклопедии чтобы напомнить себе в каких случаях физика любит обращаться к этому явлению то смотрим уже по другому на вещи типа
Пока для начала что пишут по фундаментальным и практическим свойствам ВуЗовский учебник еще в названии сообщает
| Цитата |
|---|
| Учебно-методический материал посвящен вопросам интенсивно развивающейся в последнее время теории открытых квантовых систем, являющихся одной из новых областей статистической физики. |
И уже во введении многое для чайников типа меня становится понятным
| Цитата |
|---|
| Как известно, понятие динамической системы, обладающей малым числом степеней свободы, является идеализацией. Строго говоря, в природе их не существует. Поясним сказанное на простом примере. Рассмотрим атом водорода: электрон движущийся в кулоновском поле ядра. Согласно нерелятивистской квантовой теории атом может находиться (как угодно долго) в любом из стационарных состояний. На самом деле строго стационарным является только основное состояние. С любого возбужденного уровня происходят спонтанные переходы с излучением фотона. Физическая причина этих переходов - взаимодействие с электромагнитным вакуумом, имеющим бесконечное число степеней свободы. Таким образом, атом представляет собой открытую квантовую систему. |
И когда мы смотрим на флуктуации описанные в Физической энциклопедии чтобы напомнить себе в каких случаях физика любит обращаться к этому явлению то смотрим уже по другому на вещи типа
| Цитата |
|---|
ФЛУКТУАЦИИ (от лат. fluctuatio - колебание) - случайные отклонения физ. величин от их средних значений. Ф. испытывают любые величины, зависящие от случайных факторов. Количественные характеристики Ф. основаны на методах матем. статистики и теории вероятностей. Простейшей мерой Ф. случайной величины х служит её дисперсия 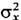 т. е. ср. квадрат отклонения х от ср. значения х, 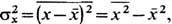 где черта сверху означает статистич. усреднение. Эквивалентной мерой Ф. является среднеквадратичное отклонение 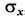 , равное корню квадратному из дисперсии, или его относит, величина 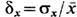 . Взаимное влияние Ф. неск. величин хi определяется их корреляциями 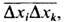 где 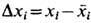 . Для статистически независимых величин 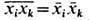 и, следовательно, корреляции равны нулю (см. также Корреляционная функция в статистич. физике). В статистич. физике Ф. вызываются хаотическим тепловым движением частиц, образующих систему. Даже в состоянии статистич. равновесия наблюдаемые физ. величины испытывают Ф. около ср. значений. С помощью Гиббса распределений как в классическом, так и в квантовом случае можно вычислить равновесные Ф. для систем, находящихся в разл. внеш. условиях; при этом Ф. выражаются через равновесные термодинамич. параметры и производные потенциалов термодинамических. Напр., для системы с пост, объёмом V и пост, числом частиц N, находящейся в контакте с термостатом (с темп-рой T), каноническое распределение даёт для Ф. энергии 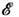 результат: 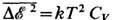 где CV - теплоёмкость системы при пост, объёме. В приведённом примере флуктуирует т. н. экстенсивная (пропорц. объёму) физ. величина - энергия. Её относит, квадратичные Ф. 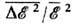 пропорциональны 1/N, т. е. очень малы. Равновесные Ф. др. экстенсивных величин (объёма, числа частиц, энтропии и т. д.) ведут себя с ро- стом числа частиц аналогичным образом. T. о., в состоянии статистич. равновесия макроскопич. величины с очень большой точностью равны своим ср. значениям |
Изменено:
Лилия Шаройко - 14.02.2018 14:05:12
