| Цитата |
|---|
| Техрук пишет: По мне виртуальность не более чем метод предсказания. |
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности.
Портал функционирует при финансовой поддержке Министерства цифрового развития, связи и массовых коммуникаций.
Важно совершенствовать математику.
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности. |
|||
|
|
Выбор также вырождается в предсказание развития событий. Целеполагание упирается в ограничение возможности прогнозировать.
Нельзя объяснить непонятное еще более непонятным
|
|||
|
|
|
Во как Трофимов-то оживился, как услышал, что меня до вечера не будет. Лучше бы он задачу решал, вместо того, чтобы
Итак, что такое момент инерции? Вики подсказывает нам, что это мера инертности тела при вращательном движении вокруг некой оси, подобно тому, как масса является мерой инертности в поступательном движении. То есть, момент инерции дает понятие, какую энергию надо будет сообщить телу, чтобы разогнать до некой нужной нам угловой скорости вокруг заданной оси. В простейшем случае - когда тело представляет из себя "маятник" с длинной стержня r и массой m сосредоточенной на его конце, момент инерции определяется как произведение массы на квадрат расстояния r 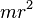 Моменты инерции прочих тел выводятся из представления о том, что тело состоит из множества таких элементарных "маятников" с элементарными массами расположеными на различных расстояниях от центра вращения. Как они выводятся можно найти в Википедии или еще где-нибудь в сети, нам это сейчас не важно. Нам Важно запомнить, что момент инерции тела равен арифметической сумме МИ составляющих его частей. Момент инерции однородного шара равен  А что будет, если шар не однородный, а состоит из слоев разной плотности, как в той задаче, что я задал Трофимову? Давайте ее решим. Итак, по условию дан шар, состоящий из свинцового ядра (11,3 г/см3) радиусом 1м и сферического слоя железа (7,8 г/см3) толщиной 1 м. Очевидно, что момент инерции такого шара по определению будет равняться арифметической сумме моментов составляющих слоев. Давайте найдем их. Если со свинцовым шаром проблем никаких нет, то для железного слоя надо будет вывести формулу. Очевидно, что момент инерции сферического слоя, ограниченного сферическими поверхностями с радисами r1 и r2 будет равняться разности моментов шаров с соответствующими радиусами и имея ввиду, что получаем А суммарный момент инерции нашего композитного шара равняется Подставляя в формулу наши значения и памятуя о соблюдении размерности, получаем 424072,8 кг*м2 При этом совокупная масса шара равняется или Подставляя значения получаем 276041 кг. Если бы мы имели однородный шар с той же массой и радиусом, то ее момент инерции согласно формуле  равнялся бы 441665,7. То есть, момент инерции однородного шара при прочих равных выше, чем у шара, плотность которого выше в центре, или, иными словами, момент инерции тела зависит не только от его геометрии, но и от распределения плотности внутри него. Но для сравнения тел, особенно имеющих разные размеры и массы, использование собственно момента инерции не очень удобно. Как сравнивать Землю и Луну? Тут-то нам и пригождается безразмерный момент инерции. Напоминаю, по определению безразмерный момент инерции - это отношение момента инерции тела к моменту инерции "маятника" с радиусом и массой на конце такой же, как и у тела. Таким образом, безразмерный момент инерции любого тела не может быть больше единицы. В принципе, можно было бы использовать для планет и отношение момента инерции к теоретическому моменту однородного, шара, но используют отношение к МИ "маятника". Итак, БМИ нашего композитного шара согласно формуле Будет равняться 0,384. Для однородной сферы, напомню, значение БМИ составляет 0,4. Если не верите, можете проверить. Итак, что мы получили? Да ровно то, что было заявлено мной с самого начала и написано во всех книгах, касающихся данного вопроса - БМИ показывает распределение плотностей внутри тела (планеты). Если планета однородная, то ее БМИ будет равняться 0,4, если плотность пород к ее центру возрастает, то БМИ будет ниже 0,4. Если бы вдруг нам повстречалась такая планета, у которой кора была бы плотнее ядра и мантии, то ее БМИ был бы больше 0,4 (но меньше 0,67). Но в природе такого, естественно, не встречается. Напоминаю, что мсье Трофимов отрицал, что БМИ что-то такое показывает, он утверждал, что БМИ зависит только от конфигурации тел, а не от распределения плотностей в них. При этом он еще и катил бочку не только на меня, но и на Википедию, МГУшные методички и, похоже, что вообще на всю планетологию и геофизику. Уже сие, даже безотносительно выкрутасов поциэнта вокруг Юпитера и всяких выковырянных из носа гигаблазаров, однозначно показывает, что мсье Трофимов - типичный science freak. Про Юпитер будет завтра.
"Чем хрупче доводы, тем тверже точка зрения" С.Е. Лец
|
|
|
|
Это осевой момент инерции, а мы рассматриваем центральный МИ. Впрочем, я не буду цепляться к словам, а предоставлю это исключительно Вам. Ляпов у Вас через слово. Путаете момент импульса с моментом инерции и прочая, в том же духе.
И вот только в этом случае, возникает понятие БМИ, как коэффициента между расчётным и действительным МИ. Действительный МИ всегда меньше расчетного более чем на 0,4, что и следует понимать как уменьшение момента инерции действительного по отношению к теоретическому для однородного шара. Теперь можно говорить о плотности тела, бессмысленному в понятии именно момента инерции. Словом, уважаемый, спутники измеряют МИ, а не БМИ, как Вы утверждаете.
Изменено:
Алексей Трофимов - 09.12.2014 09:12:34
Важно совершенствовать математику.
Внимание! Данное сообщение содержит исключительно личное мнение автора. Есть основания полагать, что оно может не отвечать критериям научности. |
|||||||||
|
|
Вы же с пеной у рта доказывали, что
Вы - фрик. В Вашем посте тоже есть ляпы, не буду их озвучивать, ищите сами. Замечу только что эта фраза
Что до вычисления БМИ при известных МИ, массе и радиусе тела, то если читатель не полный дурак, то (в отличие от Трофимова) легко сможет этот самый БМИ вычислить с помощью соответствующей формулы.
Изменено:
donPavlensio - 07.12.2014 12:53:29
"Чем хрупче доводы, тем тверже точка зрения" С.Е. Лец
|
|||||||||
|
|
|
Правильно ли я понял. что слои с одинаковой плотностью и массой могут иметь различные моменты, именно, импульса? Грубо говоря разную скорость и рычаг вектора.
donPavlensio просьба свои выкладки эмоционально не подкреплять.
Нельзя объяснить непонятное еще более непонятным
|
|
|
|
|
Уважаемые спорщики не общайтесь напрямую.
Будте ласковы апеллировать ко мне. Убедить надо меня. Пока вижу спор по терминологии.
Нельзя объяснить непонятное еще более непонятным
|
|
|
|
|
Предлагаю большую непонятку структурировать на более мелкие и удобноваривае.
Нельзя объяснить непонятное еще более непонятным
|
|
|
|
|
Абсорбировав последние выкладки, пришёл к выводу, что Алексею Трофимову недостаточно информации которую даёт БМИ для понимания каменное или же металлическое.
А что donPavlensio по этому поводу? Это если я правильно понял. 
Нельзя объяснить непонятное еще более непонятным
|
|
|
|
|
Итак, что мы имеем:
Несколько страниц форума потребовалось, чтобы вдолбить в голову величайшему гению Трофимову, что БМИ планет таки показывает распределение плотности по объему планеты. А теперь с обретенным пониманием этого факта вернемся к вычислению БМИ Юпитера, смоделированного Трофимовым. Для экономии сил я просто перепощу сюда сказанное ранее.
То есть, скальным на 90% Юпитер быть ну никак не может. Я, кстати, говорил уже, что будь Трофимов чуточку посообразительнее и покладистее, то он нашел бы значение радиуса и относительной массы скального ядра Юпитера (при средней плотности равно земной - 5,5 г/см3), которое бы удовлетворяло бы БМИ равному 0,2. Но он не нашел этой цифры. Что же, придется, как всегда, озвучивать их самому вот они: Радиус ядра 39 000 км Масса ядра 73,3% от общей массы Юпитера. Масса атмосферы 26,7% Ждем-с реакции Трофимова. Думаю, он будет радоваться такой новости.
"Чем хрупче доводы, тем тверже точка зрения" С.Е. Лец
|
|||||||||
|
|
|||||||||