Портал функционирует при финансовой поддержке Министерства цифрового развития, связи и массовых коммуникаций.
Портал функционирует при финансовой поддержке Министерства цифрового развития, связи и массовых коммуникаций.
|
Если Вы специально заранее будете подводить часы В, чтобы они к моменту прихода к А2 показывали одинаковое с ними время, то естественно они и будут это делать. Однако в этом случае они с А1 будут показывать разное время в тот момент, когда А1 и В находятся в одном месте.
|
|
|
|
|
|
|||
|
|
|
...а1....а2 ...в Одинаковое ли время будет на циферблатах "в" и "а2", когда они поравняются во втором положении: ...а1....а2 ............в
Изменено:
АСеменов - 02.03.2010 20:21:57
|
|||
|
|
|
А, вот Вы что имеете в виду
 Видите ли какая штука, пространственно разделенные события, будучи одновременными в одной системе отсчета, будут не одновременны в другой. Смотрите, что в результате получится. Дополним предыдущий рисунок еще одним моментом времени t3: 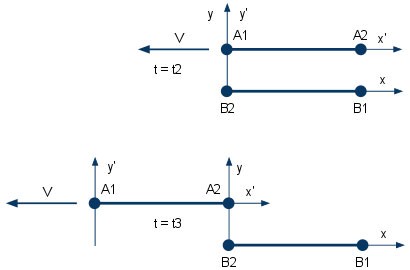 Смотрим, какие события у нас имеют место быть теперь (продолжаем нумерацию, чтобы не было потом путаницы если что). В момент t2 по времени В: 8. Часы B1 проходят мимо часов А2. В этот момент, как Вы и хотите, часы В1 синхронизируются с часами А2. 9. Часы В2 проходят мимо часов А1. Событие 9 происходит одновременно с событием 8 в системе отсчета В, поэтому часы В2 также оказываются синхронизированы с часами А2. Действительно, это сделать очень легко. Наблюдатели в В могут договориться, что когда каждый из них встречается с соответствующими часами в А, они сбрасывают показания своих часов в В на ноль. Таким образом, в тот момент, когда в системе В часы В1 совместятся с А2, а часы В2 совместятся с часами А1, то показания часов В1 и В2 окажутся равными, сброшенными до нулевого значения. Таким образом в системе отсчета В часы В2 окажутся синхронизированными с часами А2 в тот момент, когда часы В1 проходят часы А2. В точности как Вы изобразили на своей схеме в своем последнем вопросе. В момент t3 по времени В: 10. Часы В2 проходят часы А2, и наблюдатели смотрят, что у них получилось. Итак, что же у них получится? А получится, что показания часов В2 будут меньше показаний часов А2. Оба наблюдателя А2 и В2, как Вы говорите, "в упор это увидят". В самом деле, ведь система отсчета А движется относительно В, поэтому за время t3 - t2 в движущейся системе отсчета А по отношению к В должно пройти меньшее время, поэтому показания А2 должны быть меньше В2. В этом месте Вы можете обрадоваться, и сказать, дескать, ага, ведь с точки зрения наблюдателя А движется не он, а именно система отсчета В, поэтому в ней должно пройти времени меньше, тем более ведь и синхронизация была! Противоречие! Однако, нет, и я специально не все написал про события 8 и 9 выше. Вернемся к ним. События 8 и 9 происходят В РАЗНЫХ пространственных точках. Поэтому, если они одновременны в системе отсчета В, то они НЕ одновременны во всех остальных системах отсчета. Что это означает для нас? Означает повторение ситуации, которую я рассмотрел в предыдущем решении, но только теперь уже по отношению к системе отсчета А. Остановимся на том, что происходит во втором варианте задачи с точки зрения именно системы А. Обратим внимание на расстояние между точками B1 с В2 и А1 с А2. В системе отсчета В эти расстояния равны, их величина равна L. Однако, в системе отсчета А ситуация совсем иная. В ней расстояние (собственное причем) между А1 и А2 больше расстояния между В1 и В2 (вспомните, L' = L* (1/G), 1/G > 1), а значит события 8 и 9 ну никак не могут произойти одновременно. Получается, что сначала часы В2 совпадают с часами А1, и их показания устанавливаются равными нулю. Но в этот момент в системе отсчета А часы В1 еще не достигли часов А2, потому что отрезок В1-В2 короче чем А1-А2. Т.е. В1 еще не дошли до А2, а отсчет времени УЖЕ пошел. И к тому времени, когда В1 достигнет А2, уже какое-то количество времени пройдет, из-за чего к тому моменту, который изображен на второй половине нового рисунка на часах В2 "натикает" больше времени, чем на часах А2, хотя с точки зрения наблюдателей в А время в В и течет медленнее. В общем, в итоге получится, что в ситуации, изображенной на второй половине нового рисунка, будет выполняться неравенство t'3(А2) < t3(B2), что и является ответом на Ваш последний вопрос. Наблюдатель в В будет объяснять это тем, что в движущейся относительно него системе отсчета А время течет медленнее, а наблюдатель в А будет объяснять этот результат тем, что часы В2 были запущены слишком рано, "в неправильный момент времени". При желании это все тоже можно расчитать и показать итоговые формулы, как все это получается. Но пока лень. Тем более, что я в очередной раз повторяю - искать противоречия в СТО занятие совершенно бессмысленное. Возмьмите в руки мяч. Покрутите его в одну сторону, покрутите в другую сторону... Видите глазами какие-то противоречия в том, как он у Вас вращается? Может быть он становится плоским? Или передняя часть мяча убегает вперед, опережая заднюю? Нет, вращается себе и вращается. Вот ровным счетом то же самое происходит и в преобразованиях Лоренца при пересчете координат из одной системы отсчета в другую. Переход в другую систему отсчета в СТО эквивалентен повороту осей координат в пространстве Минковского. Ровным счетом такому же повороту, как и при вращении обычного мячика руками. И как при вращении мяча Вы не видите никаких несуразиц, точно также и не найдете их в СТО. |
|
|
|
|
Если на часах "а1" в этом положении "0", то на часах "а2" = dt * G + (V/c)(L'/c) ? (предположим = z) Ставим на часах "в" в этом положении= dt * G + (V/c)(L'/c) (=тоже z) .....а1....а2(z) .....в(z) Когда часы "в" проходят мимо часов "а2" Мы смотрим, какие часы отстали. (z+1) .......(z+2) ......а1....а2 (?) ...............в (?)
Изменено:
АСеменов - 02.03.2010 21:46:24
|
|||
|
|
|
Я же Вам дал весьма подробный ответ.
t'3(А2) < t3(B2) Подробности были добавлены лишь для того, чтобы объяснить детали и причины такого ответа. В переводе на Ваши обозначения будет t(А2) < t(B). |
|
|
|
|
Введем "нейтрального наблюдателя" - систему "С", которая не ускоряется и не замедляется, но относительно которой движутся и "А" и "В". Если угодно, аналог "эфира" (кажется, Вы его приверженец) или абсолютной системы отсчета. "В" ускоряется относительно "А" (догоняет его) таким образом, что в момент окончания "ускорения", относительно "С"... останавливается и сверяет свои часы с "а1", которые в тот же момент "случайно" оказались в той же точке. Что стоит, и что движется в "эфире" в этом случае? Теперь отбросим "С" (с которым мы никаких часов не сверяли), и вернемся к не раз уже изложенным рассуждениям. Что изменилось? Что теперь ЗНАЕТ "В", и что "А"? Что мешает проделать тот же трюк, "ускоряя" систему "А", и получить тот же результат? Часы, господин АСеменов, ничего не знают - они просто синхронизируются, и все. Предысторию знают (или им кажется, что "знают") часовщики, но для безмозглых приборов это не имеет никакого значения.
"Бывали хуже времена,
Но не было подлей". |
|||
|
|
Извините,это совершенно другой эксперимент. В моём эксперименте "в" ускоряется и улетает от "А", а не "догоняет".
Изменено:
АСеменов - 03.03.2010 09:55:19
|
|||
|
|
....а1....а2 ..............в Часы "в" отстают от часов "а1" "а2" (tВ < tа1, tа2 ) , Но , ссылаясь на преобразования Лоренца, часовщик "В" утверждает , что часы "А2" не синхронизированы с "а1", и , следовательно, часы "а1","а2" отстают от "в". Правильно?
Изменено:
АСеменов - 03.03.2010 10:49:53
|
|||
|
|
|
Чтобы объективно выяснить, время какой системы течёт медленнее, производим мысленный, но вполне реальный эксперимент (на вашем рисунке)
Вместе с часами (а1) и (в1) размещаем пулемёты.  Часы подают сигнал на исполняющий прИвод…прИвод жмёт на гашетку…происходит выстрел. Система А стреляет в систему (В) . Система (В) стреляет в систему (А). Частота выстрелов = 1 выстрел в секунду по часам системы. Стрелять начинают, когда часы (а1) поравняются с часами (в1). Стрельба прекращается, как только часы (а1) поравняются с (в2) ……(а2) поравняются с (в1). Если ! в системе (В) медленнее течёт время (предположим в два раза медленнее, чем в системе (А).., то система (В) и стреляет медленнее (А). Если система (А) выстрелила 10 раз. То система (В) выстрелила 5 раз. Логично? Считаем дырки.
Изменено:
АСеменов - 03.03.2010 11:22:22
|
||||
|
|
||||