Цветы глазами математика
Цветы издавна считаются символом красоты и совершенства. По словам известного математика Германа Вейля (1885—1955), человек на протяжении веков пытался постичь и то и другое посредством идеи симметрии. Как истинный учёный, он считал, что цветы достойны внимания исследователя, потому что обладают свойством поворотной симметрии, весьма распространённой в мире растений. Биологи с математиком согласны: характер симметрии в строении цветка служит одним из его существенных признаков.
Свойственная большинству цветов поворотная симметрия n-го порядка проявляется в том, что цветок совмещается сам с собой при повороте вокруг своей оси на любой из углов
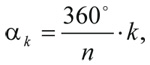
где n > 1, k = 1, 2, … , n. Что это означает в простейшем случае, когда располагающиеся по кругу лепестки образуют один слой? А вот что: всякий раз при повороте на угол 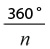
каждый лепесток встаёт на место соседнего и после n таких перемещений в одном направлении занимает исходное положение. Таким образом, порядок поворотной симметрии цветка определяется, по сути, числом его лепестков.
Например, для цветка молочая n = 2, он совмещается сам с собой при повороте на углы 180о и 360о. Для триллиума (рис. 1) и ириса n = 3, а подходящие углы поворота — 120о, 240о, 360о. Нередко встречаются цветы с поворотной симметрией 4-го порядка (сирень, чистотел), 6-го (лилия, шафран), 8-го (космея, сангвинария) и более высокого порядка, но особенно часто — 5-го (герань, лютик).
Не странно ли, что из этого стройного ряда выпадает семицветик? Природа явно отдаёт предпочтение цветам с другим числом лепестков, в частности кратным 3, 4 или 5. А может, семицветик и вовсе не был ею предусмотрен? Известно ведь, что в неживой природе у безупречно симметричных кристаллов, из которых состоят все твёрдые тела, поворотная симметрия 7-го порядка принципиально невозможна, а в животном мире из всех видов симметрии преобладает зеркальная; поворотная встречается куда реже и опять же другого порядка…
Тrientalis, он же троичник, он же седмичник
И всё-таки семицветик нашёлся! В малочисленном роду Trientalis (семейства первоцветных) всего-то три вида, из них два встречаются на территории нашей страны. Вот он — похожий на звёздочку белоснежный цветок многолетнего травянистого растения седмичник европейский (или trientalis europaea, рис. 2). Воочию полюбоваться этим обитателем елового леса можно в период цветения, приходящийся на май—июль.
Вероятно, русское название «седмичник» произошло от слова «седмь» — семь да так и закрепилось за диковинным растением: одиночный цветок с семью лепестками в природе — явление и впрямь редкостное! И даже исключительное, если учесть, что у данного растения к тому же 7 чашелистиков и 7 тычинок, в завязи выделяются 7 частей, а плод (коробочка) раскрывается 7-ю створками и нередко содержит 7 семян. Даже листьев — и тех зачастую бывает 7! Любопытно, что в толковом словаре В. Даля упоминаются и другие названия этого растения. В народе его прежде величали и семитычинником, и троичницей. Если первое название указывает на число тычинок цветка, то второе, от латинского «triens» — третья часть, говорит о другой особенности растения: длина его цветоножки составляет примерно треть от длины стебля.
Остаётся добавить, что цветки с семью лепестками встречаются и у некоторых других видов, например у печёночницы благородной (рис. 3), но чаще лепестков бывает всё-таки шесть или восемь.
Цветочные мотивы вокруг нас
Итак, в природе поворотная симметрия 7-го порядка — большая редкость. Быть может, она свойственна творениям рук человеческих? Логично было бы поискать подходящие образцы в декоративном искусстве: прикладном (вышивке, росписи, резьбе, чеканке) и монументальном, связанном с архитектурой (в витражах, мозаике, рельефах и пр.). Здесь симметрия господствует как ни в каком другом виде искусства. Свидетельства тому — художественные изделия и памятники зодчества, созданные разными народами в разные эпохи. Поворотная симметрия чётко прослеживается в круглом и круговом орнаментах, которыми украшают одежду и предметы быта, фасады и интерьеры домов и других зданий.
Во все времена одним из наиболее популярных орнаментальных мотивов был растительный, навеянный человеку самой природой. Растения для орнамента выбирались разные: египтяне часто изображали лотос и папирус, греки и римляне — листья аканта, европейцы эпохи Средневековья — трилистник и т.д.
Вот несколько примеров. Во-первых, каменные цветы. Это не только декоративные вазы и чаши, вроде тех, что изготовлял герой сказов П.Бажова Данила-мастер, но и фонтаны в парках, и венчающие колонны капители (рис. 4). Во-вторых, украшающие потолки и стены рельефные орнаменты и гипсовые розетки (рис.5). В-третьих, роскошные стеклянные витражи готических соборов: нередко их узор тоже имеет «цветочное происхождение» (рис. 6). Плоский цветочный орнамент встречается в росписи блюд и подносов, аппликации на одежде, рисунке плитки и паркета (рис. 7).
И что же мы видим? В декоративных элементах преобладает поворотная симметрия порядка n, равного или кратного 3, 4 либо 5, но никак не 7. Похожая картина наблюдается и в других случаях. Поворотная симметрия 7-го порядка не нашла отражения ни в оригинальной форме окон, ни в строении колонн, ни в конструкциях куполов и сводов, ни в общей планировке сооружений. Выходит, семицветик — диковинка не только в природе, но и в искусстве!
И всё же не бывает правил без исключений. Подтверждением тому служит орнамент с поворотной симметрией 7-го порядка, обрамлявший герб Республики Грузия (1918 —1921 гг.) (рис. 8).
Геометрия орнамента, или Как разделить круг
Почему же семицветик — такая редкость? Очевидно, всё дело в особенностях конструирования рисунка. Должно быть, секрет кроется в геометрии построений.
Правила построения эскиза круглого орнамента можно описать на языке геометрии. Для простоты ограничимся созданием плоского узора. Его легко получить, вращая вокруг заданной точки исходный элемент и копируя его. Такова общая идея.
Сначала нужно, вооружившись инструментами, разделить круг на n равных секторов и в одном из них выполнить образец рисунка. Затем повторить его в остальных частях, поворачивая каждый раз на угол 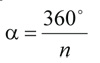
(рис. 9). Если бы мы захотели сделать эскиз семицветика, то первым делом пришлось бы разбить круг на семь равных секторов.
Проще говоря, в основе создания рисунка орнамента лежит задача о делении круга на равные части, которая сводится к разбиению на равные дуги ограничивающей круг окружности. Она известна также как задача на построение правильного многоугольника с заданным числом сторон и традиционно решается при помощи циркуля и линейки. Эта задача, кстати, стоит в одном ряду с тремя знаменитыми задачами древности: квадратурой круга, трисекцией угла и удвоением куба. И попала она туда не только благодаря своей многовековой истории, но и потому, что не всегда разрешима с помощью упомянутых инструментов.
Ещё со времён Пифагора греческие учёные проявляли интерес к правильным многоугольникам и развивали искусство их точного построения. Впоследствии эти знания были систематизированы Евклидом и изложены в IV книге «Начал». При помощи циркуля и линейки древние геометры умели строить правильные n-угольники c числом сторон, равным 3, 4, 5, 6, 8, 10, 15. При этом использовалась окружность, описанная около многоугольника.
Одни из указанных фигур можно получить на основе других. Так, имея квадрат, легко построить правильный восьмиугольник: достаточно разделить пополам каждую из четырёх дуг, на которые вершины квадрата разбивают описанную около него окружность. Всего на окружности будут отмечены восемь точек — вершин искомой фигуры. Остаётся последовательно соединить их отрезками (рис. 10).
Умея строить правильный n-угольник, нетрудно получить правильный 2n-, затем 4n-, 8n- и вообще всякий правильный (2kn)-угольник, повторяя процедуру деления необходимое число раз. Отсюда следует, что достаточно решить исходную задачу для правильных многоугольников с нечётным числом сторон.
А вот правильный n-угольник, для которого n = km, а числа k и m взаимно просты (то есть не имеют общих делителей, кроме 1), можно построить на основе двух правильных многоугольников — с числом сторон k и m, вписанных в одну окружность. В «Началах» Евклида приводится решение этой задачи для пятнадцатиугольника (15 = 3 ⋅ 5).
И всё-таки он делится!
Во многих случаях ни первый, ни второй способ не годится, как, впрочем, и другие. Скажем, правильный девятиугольник был бы построен, если бы удалось разделить на три равные части каждую из дуг, на которые разбивают описанную окружность вершины равностороннего треугольника. Однако точно это сделать нельзя: при помощи циркуля и линейки задача неразрешима (доказано, что трисекция угла 120о невозможна). Безуспешными оказались и попытки решить задачу для ряда других значений n, в том числе n = 7. Неизвестно было даже, осуществимо ли такое построение в принципе.
Ответ на вопрос, занимавший геометров почти 2300 лет, был дан только в 1796 году. 18-летний Карл Фридрих Гаусс (будущий «король математиков»), доказал, что при помощи циркуля и линейки правильный n-угольник с нечётным числом сторон можно построить лишь в том случае, когда n — простое число вида 22k +1 или является произведением различных простых чисел указанного вида.
Отметим, что при n = 3, 5, 15 задача покорилась ещё древним грекам, при n = 17 — всё тому же Гауссу. Но она так и останется невыполнимой для n = 7, 9, 11, 13 и многих других чисел. Выходит, построить при помощи двух основных ин-струментов снежинку, трилистник или пятиконечную звезду можно, а вот нарисовать «правильный» семицветик не получится.
Что ж, деваться некуда. Придётся пожертвовать этой самой «правильностью». Точность, которую так ценят математики, — это, конечно, хорошо, но в действительности достигнуть её бывает сложнее, чем кажется. Скажем, разделить круг на 3, 4 или 6 равных секторов — задача нетрудная, но с делением на 5 частей справится уже далеко не каждый. Другое дело — освоить для практических нужд какой-нибудь более простой и, что важно, пригодный в разных ситуациях приближённый метод решения задачи. Главное, чтобы он обеспечивал достаточно точный результат.
Вот один из подходящих методов деления окружности на n частей, для которого при n ≤ 10 погрешность построения не превышает 1%. На диаметре АВ окружности построим равносторонний треугольник ABC, разделим основание AB на n равных частей. Затем проведём из вершины C через вторую точку деления луч до пересечения с окружностью — получим точку D. Тогда дуга AD составит 1/n часть окружности, а хорда AD будет стороной правильного n-угольника.
Применим этот метод в случае n = 7 (рис. 11). Две точки деления — A и D уже есть, отметим при помощи циркуля остальные пять точек (раствор циркуля, которым делаются засечки на окружности, берём равным AD). Наконец, соединим каждую из семи точек с центром окружности. Заготовка для семицветика готова, дело за малым — придумать и нарисовать узор из лепестков!
Фото предоставлены автором.




